【題目】如圖，AB為圓O的直徑，點E，F在圓O上，
，矩形ABCD和圓O所在的平面互相垂直，已知
，
．
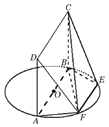
求證：平面
平面CBF；
當
時，求多面體FABCD的體積．
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，滿足
，
，數列
滿足
，，且
.
（1）求數列的通項公式；
（2）求證：數列
是等差數列，求數列的通項公式；
（3）若
，數列
的前項和為
，對任意的，都有
，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某科室安排甲、乙、丙、丁四人國慶節放假期間（共放假八天）的值班表.已知甲、乙各值班四天，甲不能在第一天值班且甲、乙不在同一天值班；丙需要值班三天，且不能連續值班；丁需要值班五天；規定每天必須兩人值班.則符合條件的不同方案共有（ ）種.
A. 400 B. 700 C. 840 D. 960
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知動點M與到點N(3，0)的距離比動點M到直線x=-2的距離大1，記動圓M的軌跡為曲線C.
(1)求曲線C的方程;
(2)若直線l與曲線C相交于A，B:兩點，且
(O為坐標原點)，證明直線l經過定點H，并求出H點的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：
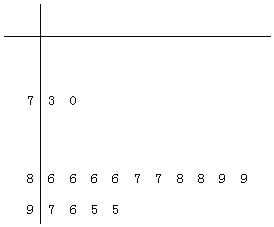
【題目】陜西理工大學開展大學生社會實踐活動，用“10分制”隨機調查漢臺區某社區居民的幸福指數，現從調查人群中隨機抽取16人，如圖所示的莖葉圖記錄了他們的幸福指數的得分
以小數點的前一位數字為莖，小數點后的一位數字為葉
：
寫出這組數據的眾數和中位數；
若幸福指數不低于9分，則稱該人的幸福指數為“極幸福”；若幸福指數不高于8分，則稱該人的幸福指數為“不夠幸福”
現從這16人中幸福指數為“極幸福”和“不夠幸福”的人中任意選取2人，求選出的兩人的幸福指數均為“極幸福”的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經觀測，某公路段在某時段內的車流量
(千輛/小時)與汽車的平均速度
(千米/小時)之間有函數關系：
．
（1）在該時段內，當汽車的平均速度為多少時車流量最大？最大車流量為多少？(精確到0.01)
（2）為保證在該時段內車流量至少為10千輛/小時，則汽車的平均速度應控制在什么范圍內？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝x2－mlnx，h(x)＝x2－x＋a.
(1)當a＝0時，f(x)≥h(x)在(1，＋∞)上恒成立，求實數m的取值范圍；
(2)當m＝2時，若函數k(x)＝f(x)－h(x)在區間(1,3)上恰有兩個不同零點，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
，圓
，一動圓在
軸右側與
軸相切，同時與圓
相外切，此動圓的圓心軌跡為曲線C，曲線E是以
，
為焦點的橢圓。
（1）求曲線C的方程；
（2）設曲線C與曲線E相交于第一象限點P，且
，求曲線E的標準方程；
（3）在（1）、（2）的條件下，直線
與橢圓E相交于A，B兩點，若AB的中點M在曲線C上，求直線
的斜率
的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
