
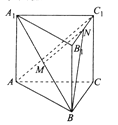
【題目】如圖,在直三棱柱![]() 中,
中, ![]() 分別是
分別是![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)若三棱柱![]() 的體積為4,求異面直線
的體積為4,求異面直線![]() 與
與![]() 夾角的余弦值.
夾角的余弦值.
科目:高中數學 來源: 題型:
【題目】四棱錐![]() 的底面ABCD是邊長為a的菱形,
的底面ABCD是邊長為a的菱形,![]() 面ABCD,
面ABCD,![]() ,E,F分別是CD,PC的中點.
,E,F分別是CD,PC的中點.

(1)求證:平面![]() 平面PAB;
平面PAB;
(2)M是PB上的動點,EM與平面PAB所成的最大角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A,B是R中兩個子集,對于![]() ,定義:
,定義: 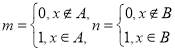 .①若
.①若![]() ;則對任意
;則對任意![]() ;②若對任意
;②若對任意![]() ,則
,則![]() ;③若對任意
;③若對任意![]() ,則A,B的關系為
,則A,B的關系為![]() .上述命題正確的序號是______. (請填寫所有正確命題的序號)
.上述命題正確的序號是______. (請填寫所有正確命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】標號為0到9的10瓶礦泉水.
(1)從中取4瓶,恰有2瓶上的數字相鄰的取法有多少種?
(2)把10個空礦泉水瓶掛成如下4列的形式,作為射擊的靶子,規定每次只能射擊每列最下面的一個(射中后這個空瓶會掉到地下),把10個礦泉水瓶全部擊中有幾種不同的射擊方案?
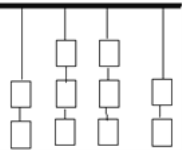
(3)把擊中后的礦泉水瓶分送給A、B、C三名垃圾回收人員,每個瓶子1角錢.垃圾回收人員賣掉瓶子后有幾種不同的收入結果?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成.將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級.參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%.選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績.
某校高一年級共2000人,為給高一學生合理選科提供依據,對六個選考科目進行測試,其中物理考試原始成績基本服從正態分布N(60,169).
(Ⅰ)求物理原始成績在區間(47,86)的人數;
(Ⅱ)按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間[61,80]的人數,求X的分布列和數學期望.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《山東省高考改革試點方案》規定:從2017年秋季高中入學的新生開始,不分文理科;2020年開始,高考總成績由語數外3門統考科目和物理、化學等六門選考科目構成.將每門選考科目的考生原始成績從高到低劃分為A、B+、B、C+、C、D+、D、E共8個等級.參照正態分布原則,確定各等級人數所占比例分別為3%、7%、16%、24%、24%、16%、7%、3%.選考科目成績計入考生總成績時,將A至E等級內的考生原始成績,依照等比例轉換法則,分別轉換到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八個分數區間,得到考生的等級成績.
某校高一年級共2000人,為給高一學生合理選科提供依據,對六個選考科目進行測試,其中物理考試原始成績基本服從正態分布N(60,169).
(Ⅰ)求物理原始成績在區間(47,86)的人數;
(Ⅱ)按高考改革方案,若從全省考生中隨機抽取3人,記X表示這3人中等級成績在區間[61,80]的人數,求X的分布列和數學期望.
(附:若隨機變量![]() ,則
,則![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() ,把圓
,把圓![]() 上每一點的橫坐標伸長為原來的2倍,縱坐標不變,得到曲線
上每一點的橫坐標伸長為原來的2倍,縱坐標不變,得到曲線![]() ,且傾斜角為
,且傾斜角為![]() ,經過點
,經過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)當![]() 時,求曲線
時,求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的參數方程;
的參數方程;
(2)求點![]() 到
到![]() 兩點的距離之積的最小值.
兩點的距離之積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若a=0時,求函數![]() 的零點;
的零點;
(2)若a=4時,求函數![]() 在區間[2,5]上的最大值和最小值;
在區間[2,5]上的最大值和最小值;
(3)當![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com