
【題目】已知函數![]() .
.
(1)若a=0時,求函數![]() 的零點;
的零點;
(2)若a=4時,求函數![]() 在區間[2,5]上的最大值和最小值;
在區間[2,5]上的最大值和最小值;
(3)當![]() 時,不等式
時,不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
【答案】(1)x=1 (2) 函數![]() 的最大值為12,最小值為5. (3)
的最大值為12,最小值為5. (3) ![]()
【解析】
(1)當![]() 時,去絕對值變分段函數,再求
時,去絕對值變分段函數,再求![]() 的根,即為函數零點;(2)當
的根,即為函數零點;(2)當![]() 時,
時,![]() ;再對
;再對![]() 的取值進行分類討論去掉絕對值符號:①當
的取值進行分類討論去掉絕對值符號:①當![]() 時,②當
時,②當![]() 時,分別求出在各自區間上的最值,最后綜合得到函數
時,分別求出在各自區間上的最值,最后綜合得到函數![]() 的最值;(3)將已知條件等價轉化為
的最值;(3)將已知條件等價轉化為![]() 恒成立,下面只要利用分離參數法求出函數
恒成立,下面只要利用分離參數法求出函數![]() 和
和![]() 在給定區間上的最值即得.
在給定區間上的最值即得.
(1)當![]() 時,
時,![]()
由![]() 得x=1或x=-3(舍),
得x=1或x=-3(舍),
由![]() 得方程無解,
得方程無解,
綜上得,函數![]() 的零點為x=1;
的零點為x=1;
(2)當![]() 時,
時,![]() ;
;
①當![]() 時,
時,![]() ,
,
當x=2時,![]() ;當x=3時,
;當x=3時,![]() ;
;
②當4≤x≤5時,![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
綜上可知:函數![]() 的最大值為12,最小值為5.
的最大值為12,最小值為5.
(3)若![]() ,原不等式化為
,原不等式化為![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,即
,即![]() ,
,
若![]() ,原不等式化為
,原不等式化為![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() ,即
,即![]() ,
,
綜上可知:a的取值范圍為![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,下圖(1)、(2)、(3)、(4)為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含f(n)個小正方形.
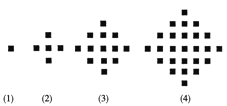
(1) 求出![]() ,
,![]() ,
,![]() 并猜測
并猜測![]() 的表達式;
的表達式;
(2) 求證:![]() +
+![]() +
+![]() +…+
+…+![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年被稱為“新高考元年”,隨著上海、浙江兩地順利實施“語數外+3”新高考方案,新一輪的高考改革還將繼續在全國推進。遼寧地區也將于2020年開啟新高考模式,今年秋季入學 的高一新生將面臨從物理、化學、生物、政治、歷史、地理等6科中任選三科(共20種選法)作為 自己將來高考“語數外+3 ”新高考方案中的“3”。某地區為了順利迎接新高考改革,在某學校理科班的200名學生中進行了“學生模擬選科數據”調查,每個學生只能從表格中的20種課程 組合選擇一種學習。模擬選課數據統計如下表:
序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
組合學科 | 物化生 | 物化政 | 物化歷 | 物化地 | 物生政 | 物生歷 | 物生地 |
人數 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序號 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
組合學科 | 物政歷 | 物政地 | 物歷地 | 化生政 | 化生歷 | 化生地 | 化政歷 |
人數 | 5人 | 0人 | 5人 | ... | 40人 | ... | ... |
序號 | 15 | 16 | 17 | 18 | 19 | 20 | |
組合學科 | 化政地 | 化歷地 | 生政歷 | 生政地 | 生歷地 | 政歷地 | 總計 |
人數 | ... | ... | ... | ... | ... | ... | 200人 |
為了解學生成績與學生模擬選課情之間的關系,用分層抽樣的方法從這200名學生中抽取40人的樣本進行分析.
(1)樣本中選擇組合12號“化生歷”的有多少人?樣本中選擇學習物理的有多少人?
(2)從樣本選擇學習地理且學習物理的學生中隨機抽取3人,求這3人中至少有1人還要學習生物的概率;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以原點為極點,
為參數),以原點為極點, ![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標系,曲線
軸的正半軸為極軸,以相同的長度單位建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求直線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,若
兩點,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于回歸分析的說法中錯誤的有( )個
(1). 殘差圖中殘差點所在的水平帶狀區域越寬,則回歸方程的預報精確度越高.
(2). 回歸直線一定過樣本中心![]() 。
。
(3). 兩個模型中殘差平方和越小的模型擬合的效果越好。
(4) .甲、乙兩個模型的![]() 分別約為0.88和0.80,則模型乙的擬合效果更好.
分別約為0.88和0.80,則模型乙的擬合效果更好.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與正切函數
與正切函數![]() 相鄰兩支曲線的交點的橫坐標分別為
相鄰兩支曲線的交點的橫坐標分別為![]() ,
, ![]() ,且有
,且有![]() ,假設函數
,假設函數![]() 的兩個不同的零點分別為
的兩個不同的零點分別為![]() ,
, ![]() ,若在區間
,若在區間![]() 內存在兩個不同的實數
內存在兩個不同的實數![]() ,
, ![]() ,與
,與![]() ,
, ![]() 調整順序后,構成等差數列,則
調整順序后,構成等差數列,則![]() 的值為( )
的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() 或不存在 D.
或不存在 D. ![]() 或
或![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某校甲、乙、丙三個年級的學生志愿者人數分別為240,160,160.現采用分層抽樣的方法從中抽取7名同學去某敬老院參加獻愛心活動.
(Ⅰ)應從甲、乙、丙三個年級的學生志愿者中分別抽取多少人?
(Ⅱ)設抽出的7名同學分別用A,B,C,D,E,F,G表示,現從中隨機抽取2名同學承擔敬老院的衛生工作.
(i)試用所給字母列舉出所有可能的抽取結果;
(ii)設M為事件“抽取的2名同學來自同一年級”,求事件M發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,PD⊥平面ABCD,![]() ,∠ABC=∠BCD=90°,E為PB的中點。
,∠ABC=∠BCD=90°,E為PB的中點。

(1)證明:CE∥面PAD.
(2)若直線CE與底面ABCD所成的角為45°,求四棱錐P-ABCD的體積。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com