Question

【題目】已知三棱柱的側棱垂直于底面，，，，，分別是，的中點.

（Ⅰ）證明：平面；

（Ⅱ）求二面角的余弦值.

Answer 1

【答案】(1)見解析;(2).

【解析】分析：解法一：依題意可知兩兩垂直，以點為原點建立空間直角坐標系，

（1）利用直線的方向向量和平面的法向量垂直，即可證得線面平面；

（2）求出兩個平面的法向量，利用兩個向量的夾角公式，即可求解二面角的余弦值.

解法二：利用空間幾何體的點線面位置關系的判定定理和二面角的定義求解：

（1）設的中點為，連接，證明四邊形為平行四邊形，得出線線平行，利用線面平行的判定定理即可證得線面平面；

（2）以及二面角的平面角，在直角三角形中求出其平面角的余弦值，即可得到二面角的余弦值.

詳解：解法一：依條件可知、、兩兩垂直，

如圖，以點為原點建立空間直角坐標系.

根據條件容易求出如下各點坐標：，，，，，，，.

（Ⅰ）證明：∵，，

是平面的一個法向量，且，

所以.

又∵平面，∴平面；

（Ⅱ）設是平面的法向量，

因為，，

由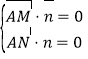，得.

解得平面的一個法向量，

由已知，平面的一個法向量為，

，

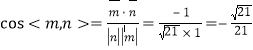∴二面角的余弦值是.

解法二：

（Ⅰ）證明：設的中點為，連接，，

∵，分別是，的中點，∴，

又∵，，

∴，∴四邊形是平行四邊形，

∴，∵平面，平面，

∴平面；

（Ⅱ）如圖，設的中點為，連接，

∴，∵底面，∵，，∴，，

∴，∴底面，

在平面內，過點做，垂足為，

連接，，，，

∴平面，則，

∴是二面角的平面角，

∵，由，得，

所以，所以，

∴二面角的余弦值是.