
���}Ŀ����ֱ֪��l1�ķ��̞�3x+4y��12=0��
��1����ֱ��l2�cl1ƽ�У����^(gu��)�c(di��n)����1��3������ֱ��l2�ķ��̣�
��2����ֱ��l2�cl1��ֱ����l2�c������(bi��o)�S���ɵ���������e��4����ֱ��l2�ķ��̣�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]()
����������������1������(j��)ƽ��ֱ����б����ȣ������б�ʣ��c(di��n)бʽ���ֱ�����̣���2������(j��)��ֱ�P(gu��n)ϵ���ֱ����б�ʣ��õ���������(bi��o)�S�ϵĽؾ࣬����(j��)�c������(bi��o)�S���ɵ���������e��4���ؾ࣬����ֱ�����̣�
Ԕ������1����ֱ��l2�cl1ƽ�У����O(sh��)l2�ķ��̞�3x+4y+m=0����x=��1��y=3���룬�é�3+12+m=0������m=��9��
��ֱ��l2�ķ��̞�3x+4y��9=0��
��2����ֱ��l2�cl1��ֱ�����O(sh��)l2�ķ��̞�4x��3y+n=0��
��y=0����x=��![]() ����x=0����y=
����x=0����y=![]() ��
��
����������eS=![]() |��
|��![]() ||
||![]() |=4
|=4
����n2=96����n=��4![]()
��ֱ��l2�ķ�����4x��3y+4![]() =0��4x��3y��4
=0��4x��3y��4![]() =0��
=0��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У���A��B��C�Č�(du��)߅�քe��a��b��c���ң�c��2a�� ![]() =c
=c ![]()
![]()
��1����B�Ĵ�С��
��2����֪f��x��=cosx��asinx��2cosx��+1����(du��)�����x��R������f��x����f��B������(sh��)f��x���Ć��{(di��o)�f�p�^(q��)�g��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
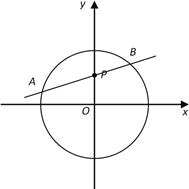
���}Ŀ����D����֪?ji��ng)�ֱ��![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() �����c�A
�����c�A![]() ����
����![]() ��
��![]() ���c(di��n)��
���c(di��n)��
��1����ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ����
����![]() ����e��
����e��
��2����ֱ��![]() ��б�ʞ�
��б�ʞ�![]() ���c(di��n)
���c(di��n)![]() �LjA
�LjA![]() ������һ�c(di��n)����
������һ�c(di��n)����![]() ��ȡֵ������
��ȡֵ������
��3���Ƿ����һ��(g��)���c(di��n)![]() ����ͬ���c(di��n)
����ͬ���c(di��n)![]() ������(du��)�����ⲻ�c
������(du��)�����ⲻ�c![]() �S�غϵ�ֱ��
�S�غϵ�ֱ��![]() ������
������![]() ƽ��
ƽ��![]() �������ڣ�������c(di��n)
�������ڣ�������c(di��n)![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����![]() ��
��![]() ��ӛ
��ӛ![]() ��ͬ�r(sh��)�M�����Зl���ļ���
��ͬ�r(sh��)�M�����Зl���ļ���![]() �Ă�(g��)��(sh��)��
��(g��)��(sh��)��
��![]() ������
������![]() ���t
���t![]() ������
������![]() ���t
���t![]() ��
��
�t��![]() ��
��![]() ___________��
___________��
��![]() ��
��![]() �Ľ���ʽ����
�Ľ���ʽ����![]() ��ʾ��
��ʾ��![]() ___________��
___________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=|x��a|+|x+5��a|
��1��������ʽf��x����|x��a|��2�Ľ⼯��[��5����1]����(sh��)��(sh��)a��ֵ��
��2����x0��R��ʹ��f��x0����4m+m2 �� ��(sh��)��(sh��)m��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=asinx![]() cos2x+1��a��b��R����
cos2x+1��a��b��R����
��1����(d��ng)a=1����![]()
![]() �r(sh��)����f��x����ֵ��
�r(sh��)����f��x����ֵ��
��2�������ڌ�(sh��)��(sh��)![]()
![]() ʹ��
ʹ��![]() ��������(sh��)��(sh��)a��ȡֵ������
��������(sh��)��(sh��)a��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����У��һ�꼉(j��)�о��ԌW(xu��)��(x��)С�M����9���W(xu��)����������3��������6��Ů��.���о��ԌW(xu��)��(x��)�^(gu��)���У�Ҫ�M(j��n)�Ѓɴ΅R��(b��o)���(d��ng)�����_(k��i)�}�R��(b��o)�ͽY(ji��)�}�R��(b��o)����ÿ�΅R��(b��o)�����@9���W(xu��)�����S�C(j��)�x1 ����������l(f��)��.�O(sh��)ÿ��ÿ�α��x���c�������Ӱ�.
��1����ɴ΅R��(b��o)���(d��ng)����С�M�ɆT�װl(f��)�Եĸ��ʣ�
��2���O(sh��)![]() �������l(f��)�ԴΔ�(sh��)�cŮ���l(f��)�ԴΔ�(sh��)֮��Ľ^��(du��)ֵ����
�������l(f��)�ԴΔ�(sh��)�cŮ���l(f��)�ԴΔ�(sh��)֮��Ľ^��(du��)ֵ����![]() �ķֲ��к͔�(sh��)�W(xu��)����.
�ķֲ��к͔�(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() .
.
��1��������(sh��)![]() �ͺ���(sh��)
�ͺ���(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() �Ͼ���������(sh��)����(sh��)��(sh��)
�Ͼ���������(sh��)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��2��������![]() ��Ψһ�⣬��(sh��)��(sh��)
��Ψһ�⣬��(sh��)��(sh��)![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪���タ![]() �Ľ��c(di��n)��
�Ľ��c(di��n)��![]() ���c(di��n)
���c(di��n)![]() �ڒ��タ
�ڒ��タ![]() �ϣ���
�ϣ���![]() ��
��
���������タ![]() �Ę�(bi��o)��(zh��n)���̼���(sh��)��(sh��)
�Ę�(bi��o)��(zh��n)���̼���(sh��)��(sh��)![]() ��ֵ��
��ֵ��
������ֱ��![]() �^(gu��)���タ
�^(gu��)���タ![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() �����c���タ
�����c���タ![]() ����
����![]() ���c(di��n)����
���c(di��n)����![]() ��
��![]() ������(bi��o)ԭ�c(di��n)������e��
������(bi��o)ԭ�c(di��n)������e��![]() ����ֱ��
����ֱ��![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com