
【題目】已知橢圓![]() 的方程為
的方程為![]() ,
,![]() 在橢圓上,橢圓的左頂點為
在橢圓上,橢圓的左頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 倍.
倍.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() (
(![]() )與橢圓
)與橢圓![]() 交于
交于![]() ,
,![]() ,連接
,連接![]() ,
,![]() 并延長交橢圓
并延長交橢圓![]() 于
于![]() ,
,![]() ,連接
,連接![]() ,指出
,指出![]() 與
與![]() 之間的關系,并說明理由.
之間的關系,并說明理由.
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,點E在棱AB上移動.
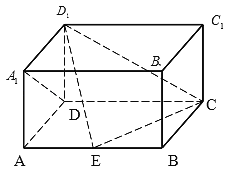
(1)證明:D1E⊥A1D;
(2)若EB![]() ,求二面角D1﹣EC﹣D的大小.
,求二面角D1﹣EC﹣D的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 對于任意的
對于任意的![]()
![]() ,都有
,都有![]() ,當
,當![]() 時,
時,![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)當![]() 時,求函數
時,求函數![]() 的最大值和最小值;
的最大值和最小值;
(3)設函數![]() ,判斷函數g(x) 最多有幾個零點,并求出此時實數m的取值范圍.
,判斷函數g(x) 最多有幾個零點,并求出此時實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】手機![]() 中的“
中的“![]() 運動”具有這樣的功能,不僅可以看自己每天的運動步數,還可以看到朋友圈里好友的步數.小明的
運動”具有這樣的功能,不僅可以看自己每天的運動步數,還可以看到朋友圈里好友的步數.小明的![]() 朋友圈里有大量好友參與了“
朋友圈里有大量好友參與了“![]() 運動”,他隨機選取了其中30名,其中男女各15名,記錄了他們某一天的走路步數,統計數據如下表所示:
運動”,他隨機選取了其中30名,其中男女各15名,記錄了他們某一天的走路步數,統計數據如下表所示:
|
|
|
|
|
|
男 | 0 | 2 | 4 | 7 | 2 |
女 | 1 | 3 | 7 | 3 | 1 |
(Ⅰ)以樣本估計總體,視樣本頻率為概率,在小明![]() 朋友圈里的男性好友中任意選取3名,其中走路步數低于7500步的有
朋友圈里的男性好友中任意選取3名,其中走路步數低于7500步的有![]() 名,求
名,求![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)如果某人一天的走路步數超過7500步,此人將被“![]() 運動”評定為“積極型”,否則為“消極型”.根據題意完成下面的
運動”評定為“積極型”,否則為“消極型”.根據題意完成下面的![]() 列聯表,并據此判斷能否有
列聯表,并據此判斷能否有![]() 以上的把握認為“評定類型”與“性別”有關?
以上的把握認為“評定類型”與“性別”有關?
積極型 | 消極型 | 總計 | |
男 | |||
女 | |||
總計 |
附:![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南北朝數學家何承天發明的“調日法”是程序化尋求精確分數來表示數值的算法,其理論依據是:設實數![]() 的不足近似值和過剩近似值分別為
的不足近似值和過剩近似值分別為![]() 和
和![]()
![]() ,則
,則![]() 是
是![]() 的更為精確的近似值.
的更為精確的近似值.
我們知道![]() ,我國早在《周髀算經》中就有“周三徑一”的古率記載,《隋書律歷志》有如下記載:“南徐州從事史祖沖之更開密法,以圓徑一億為丈,圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,肭數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈肭二限之間。密率:圓徑一百一十三,圓周三百五十五。約率,圓徑七,周二十二”,這一記錄指出了祖沖之關于圓周率的兩大貢獻:其一是求得圓周率
,我國早在《周髀算經》中就有“周三徑一”的古率記載,《隋書律歷志》有如下記載:“南徐州從事史祖沖之更開密法,以圓徑一億為丈,圓周盈數三丈一尺四寸一分五厘九毫二秒七忽,肭數三丈一尺四寸一分五厘九毫二秒六忽,正數在盈肭二限之間。密率:圓徑一百一十三,圓周三百五十五。約率,圓徑七,周二十二”,這一記錄指出了祖沖之關于圓周率的兩大貢獻:其一是求得圓周率![]() ;其二是得到
;其二是得到![]() 的兩個近似分數即:約率為22/7,密率為355/113,他算出的
的兩個近似分數即:約率為22/7,密率為355/113,他算出的![]() 的8位可靠數字,不但在當時是最精密的圓周率,而且保持世界紀錄一千多年,他對
的8位可靠數字,不但在當時是最精密的圓周率,而且保持世界紀錄一千多年,他對![]() 的研究真可謂“運籌于帷幄之中,決勝于千年之外”,祖沖之是我國古代最有影響的數學家之一,莫斯科大學走廊里有其塑像,1959年10月,原蘇聯通過“月球3”號衛星首次拍下月球背面照片后,就以祖沖之命名一個環形山,其月面坐標是:東經148度,北緯17度.
的研究真可謂“運籌于帷幄之中,決勝于千年之外”,祖沖之是我國古代最有影響的數學家之一,莫斯科大學走廊里有其塑像,1959年10月,原蘇聯通過“月球3”號衛星首次拍下月球背面照片后,就以祖沖之命名一個環形山,其月面坐標是:東經148度,北緯17度.
縱橫古今,關于![]() 值的研究,經歷了古代試驗法時期、幾何法時期、分析法時期、蒲豐或然性試驗方法時期、計算機時期,己知
值的研究,經歷了古代試驗法時期、幾何法時期、分析法時期、蒲豐或然性試驗方法時期、計算機時期,己知![]() ,試以上述
,試以上述![]() 的不足近似值
的不足近似值![]() 和過剩近似值
和過剩近似值![]() 為依據,那么使用兩次“調日法”后可得
為依據,那么使用兩次“調日法”后可得![]() 的近似分數為____________
的近似分數為____________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中正確的是______.
(1)將![]() 圖像向左平移
圖像向左平移![]() 個單位,再將所有點的橫坐標擴大為原來的
個單位,再將所有點的橫坐標擴大為原來的![]() 倍,得到
倍,得到![]() 的圖像;
的圖像;
(2)將![]() 圖像上所有點的橫坐標擴大為原來的
圖像上所有點的橫坐標擴大為原來的![]() 倍,再將圖像向左平移
倍,再將圖像向左平移![]() 個單位,得到
個單位,得到![]() 的圖像;
的圖像;
(3)將![]() 圖像上所有點的橫坐標擴大為原來的
圖像上所有點的橫坐標擴大為原來的![]() 倍,再將圖像向左平移
倍,再將圖像向左平移![]() 個單位,得到
個單位,得到![]() 的圖像;
的圖像;
(4)將![]() 圖像上所有點的橫坐標變為原來的
圖像上所有點的橫坐標變為原來的![]() 倍,再將圖像向左平移
倍,再將圖像向左平移![]() 個單位,得到
個單位,得到![]() 的圖像;
的圖像;
(5)將![]() 圖像向左平移
圖像向左平移![]() 個單位,再將所有點的橫坐標擴大為原來的
個單位,再將所有點的橫坐標擴大為原來的![]() 倍,得到
倍,得到![]() 的圖像;
的圖像;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,點
,點![]() 在直線
在直線![]() 上,其中
上,其中![]() .
.
(1)令![]() ,求證數列
,求證數列![]() 是等比數列;
是等比數列;
(2)求數列![]() 的通項;
的通項;
(3)設![]() 、
、![]() 分別為數列
分別為數列![]() 、
、![]() 的前
的前![]() 項和是否存在實數
項和是否存在實數![]() ,使得數列
,使得數列![]() 為等差數列?若存在,試求出
為等差數列?若存在,試求出![]() ,若不存在,則說明理由.
,若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知圓![]() 的圓心為
的圓心為![]() ,半徑為
,半徑為![]() .以極點為原點,極軸方向為
.以極點為原點,極軸方向為![]() 軸正半軸方向,利用相同單位長度建立平面直角坐標系,直線
軸正半軸方向,利用相同單位長度建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數,
為參數,![]() 且
且![]() ).
).
(Ⅰ)寫出圓![]() 的極坐標方程和直線
的極坐標方程和直線![]() 的普通方程;
的普通方程;
(Ⅱ)若直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 底面
底面![]() ,底面
,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
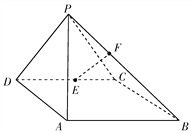
(Ⅰ)求證: ![]() ;
;
(Ⅱ)試確定點![]() 的位置,使得直線
的位置,使得直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等.
所成的角相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com