
【題目】一臺機器由于使用時間較長,生產的零件有一些會有缺損,按不同轉速生產出來的零件有缺損的統計數據如表所示:

(1)作出散點圖;
(2)如果![]() 與
與![]() 線性相關,求出回歸直線方程.
線性相關,求出回歸直線方程.
(3)若實際生產中,允許每小時的產品中有缺損的零件最多為10個,那么,機器的運轉速度應控制在什么范圍內?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為,
的斜率和截距的最小二乘估計分別為,
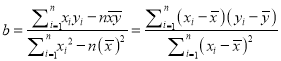 ,
, ![]()
 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案科目:高中數學 來源: 題型:
【題目】共享單車是指由企業在校園、公交站點、商業區、公共服務區等場所提供的自行車單車共享服務,由于其依托“互聯網+”,符合“低碳出行”的理念,已越來越多地引起了人們的關注.某部門為了對該城市共享單車加強監管,隨機選取了100人就該城市共享單車的推行情況進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[50,60),[60,70),…,[90,100] 分成5組,制成如圖所示頻率分直方圖.
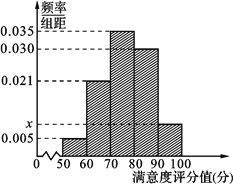
(1) 求圖中![]() 的值;
的值;
(2) 已知滿意度評分值在[90,100]內的男生數與女生數的比為2:1,若在滿意度評分值為[90,100]的人中隨機抽取4人進行座談,設其中的女生人數為隨機變量![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某中學聯盟舉行了一次“盟校質量調研考試”活動,為了解本次考試學生的某學科成績情況,從中抽取部分學生的分數(滿分為![]() 分,得分取正整數,抽取學生的分數均在
分,得分取正整數,抽取學生的分數均在![]() 之內)作為樣本(樣本容量為
之內)作為樣本(樣本容量為![]() )進行統計,按照
)進行統計,按照![]() 的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在
的分組作出頻率分布直方圖,并作出樣本分數的莖葉圖(莖葉圖中僅列出了得分在![]() 的數據)
的數據)
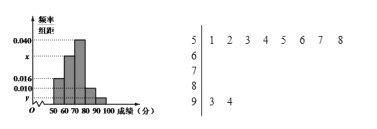
(Ⅰ)求樣本容量![]() 和頻率分布直方圖中的
和頻率分布直方圖中的![]() 的值;
的值;
(Ⅱ)在選取的樣本中,從成績在![]() 分以上(含
分以上(含![]() 分)的學生中隨機抽取
分)的學生中隨機抽取![]() 名學生參加“省級學科基礎知識競賽”,求所抽取的
名學生參加“省級學科基礎知識競賽”,求所抽取的![]() 名學生中恰有一人得分在
名學生中恰有一人得分在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:在數列![]() 中,若
中,若![]() 為常數)則稱
為常數)則稱![]() 為“等方差數列”,下列是對“等方差數列”的有關判斷( )
為“等方差數列”,下列是對“等方差數列”的有關判斷( )
①若![]() 是“等方差數列”,在數列
是“等方差數列”,在數列![]() 是等差數列;
是等差數列;
②![]() 是“等方差數列”;
是“等方差數列”;
③若![]() 是“等方差數列”,則數列
是“等方差數列”,則數列![]() 為常)也是“等方差數列”;
為常)也是“等方差數列”;
④若![]() 既是“等方差數列”又是等差數列,則該數列是常數數列.
既是“等方差數列”又是等差數列,則該數列是常數數列.
其中正確命題的個數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“石頭、剪刀、布”是個廣為流傳的游戲,游戲時甲乙雙方每次做“石頭”“剪刀”“布”三種手勢中的一種,規定:“石頭”勝“剪刀”,“剪刀”勝“布”,“布”勝“石頭”,同種手勢不分勝負須繼續比賽,假設甲乙兩人都是等可能地做這三種手勢.
(1)列舉一次比賽時兩人做出手勢的所有可能情況;
(2)求一次比賽甲取勝的概率,并說明“石頭、剪刀、布”這個廣為流傳的游戲的公平性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明準備利用暑假時間去旅游,媽媽為小明提供四個景點,九寨溝、泰山、長白山、武夷山.小明決定用所學的數學知識制定一個方案來決定去哪個景點:(如圖)曲線![]() 和直線
和直線![]() 交于點
交于點![]() .以
.以![]() 為起點,再從曲線
為起點,再從曲線![]() 上任取兩個點分別為終點得到兩個向量,記這兩個向量的數量積為
上任取兩個點分別為終點得到兩個向量,記這兩個向量的數量積為![]() .若
.若![]() 去九寨溝;若
去九寨溝;若![]() 去泰山;若
去泰山;若![]() 去長白山;
去長白山; ![]() 去武夷山.
去武夷山.

(1)若從![]() 這六個點中任取兩個點分別為終點得到兩個向量,分別求小明去九寨溝的概率和不去泰山的概率;
這六個點中任取兩個點分別為終點得到兩個向量,分別求小明去九寨溝的概率和不去泰山的概率;
(2)按上述方案,小明在曲線![]() 上取點
上取點![]() 作為向量的終點,則小明決定去武夷山.點
作為向量的終點,則小明決定去武夷山.點![]() 在曲線
在曲線![]() 上運動,若點
上運動,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為平面直角坐標系的原點,極軸為
,以極點為平面直角坐標系的原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 的參數方程是
的參數方程是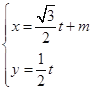 (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的的普通方程;
的的普通方程;
(2)設點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com