【題目】已知
為定義在
上的奇函數，當
時，有
，且當
時，
，下列命題正確的是（ ）
A.
B.函數在定義域上是周期為
的函數
C.直線
與函數的圖象有個交點D.函數的值域為
【答案】A
【解析】
推導出當
時，
，結合題中等式得出
，可判斷出A選項的正誤；利用特殊值法可判斷B選項的正誤；作出函數
在區間
上的圖象，利用數形結合思想可判斷C選項的正誤；求出函數在
上的值域，利用奇函數的性質可得出函數的值域，可判斷出D選項的正誤.
函數是
上的奇函數，
，由題意可得
，
當時，
，
，A選項正確；
當時，
，則
，
，
，
則函數不是上周期為
的函數，B選項錯誤；
若
為奇數時，
，
若為偶數，則
，即當
時，
，
當時，，若
，且當
時，
，
，
當
時，則
，
，
當
時，
，則
，
所以，函數在上的值域為，
由奇函數的性質可知，函數在
上的值域為，
由此可知，函數在上的值域為，D選項錯誤；
如下圖所示：
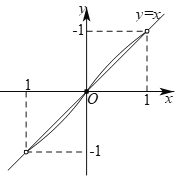
由圖象可知，當
時，函數
與函數的圖象只有一個交點，
當
或
時，
，此時，函數與函數沒有交點，
則函數與函數有且只有一個交點，C選項錯誤.
故選：A.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知函數
的圖象在點
處的切線為
，若函數滿足
（其中
為函數的定義域，當
時，
恒成立，則稱
為函數的“轉折點”，已知函數
在區間
上存在一個“轉折點”，則
的取值范圍是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（其中
為自然對數的底數）．
（1）求
的單調性；
（2）若
，對于任意
，是否存在與
有關的正常數
，使得
成立？如果存在，求出一個符合條件的；否則說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某餅屋進行為期
天的五周年店慶活動，現策劃兩項有獎促銷活動，活動一：店慶期間每位顧客一次性消費滿
元，可得
元代金券一張；活動二：活動期間每位顧客每天有一次機會獲得一個一元或兩元紅包．根據前一年該店的銷售情況，統計了
位顧客一次性消費的金額數（元），頻數分布表如下圖所示：
一次性消費金額數 |
|
|
|
|
|
人數 |
|
|
|
|
|
以這位顧客一次消費金額數的頻率分布代替每位顧客一次消費金額數的概率分布．
（1）預計該店每天的客流量為人次，求這次店慶期間，商家每天送出代金券金額數的期望；
（2）假設顧客獲得一元或兩元紅包的可能性相等，商家在店慶活動結束后會公布幸運數字，連續天參加返紅包的顧客，如果紅包金額總數與幸運數字一致，則可再獲得元的“店慶幸運紅包”一個．若公布的幸運數字是“
”，求店慶期間一位連續天消費的顧客獲得紅包金額總數的期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P-ABCD中，
平面PCD，
，
，
，E為AD的中點，AC與BE相交于點O.
（1）證明：
平面ABCD.
（2）求直線BC與平面PBD所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】人們常說的“幸福感指數”就是指某個人主觀地評價他對自己目前生活狀態的滿意程度的指標，常用區間
內的一個數來表示，該數越接近
表示滿意度越高．為了解某地區居民的幸福感情況，隨機對該地區的男、女居民各
人進行了調查，調查數據如表所示：
幸福感指數 |
|
|
|
|
|
男居民人數 |
|
|
|
|
|
女居民人數 |
|
|
|
|
|
（1）估算該地區居民幸福感指數的平均值；
（2）若居民幸福感指數不小于
，則認為其幸福．為了進一步了解居民的幸福滿意度，調查組又在該地區隨機抽取
對夫妻進行調查，用
表示他們之中幸福夫妻（夫妻二人都感到幸福）的對數，求的期望（以樣本的頻率作為總體的概率）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
