
【題目】已知長方形ABCD中,AB=3,AD=4.現將長方形沿對角線BD折起,使AC=a,得到一個四面體A-BCD,如圖所示.
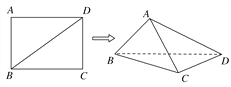
(1)試問:在折疊的過程中,直線AB與CD能否垂直?若能,求出相應a的值;若不能,請說明理由;
(2)求四面體A-BCD體積的最大值.
【答案】(1)證明見解析;(2)![]()
【解析】
試題分析:(1)假設![]() ,又
,又![]() ,則
,則![]() 平面
平面![]() ,得到
,得到![]() ,解得
,解得![]() ;(2)易知,翻折到平面
;(2)易知,翻折到平面![]() 平面
平面![]() 時,體積最大,則底面為
時,體積最大,則底面為![]() ,高為
,高為![]() ,求得最大體積為
,求得最大體積為![]() 。
。
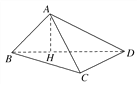
(1)直線AB與CD能夠垂直.
因為AB⊥AD,若AB⊥CD,AD∩CD=D,
則有AB⊥平面ACD,
從而AB⊥AC.
此時,a=![]() =
=![]() =
=![]() ,
,
即當a=![]() 時,有AB⊥CD.
時,有AB⊥CD.
(2)由于△BCD面積為定值,所以當點A到平面BCD的距離最大,即當平面ABD⊥平面BCD時,該四面體的體積最大,
此時,過點A在平面ABD內作AH⊥BD,垂足為H,
則有AH⊥平面BCD,AH就是該四面體的高.
在△ABD中,AH=![]() =
=![]() ,
,
S△BCD=![]() ×3×4=6,
×3×4=6,
此時VA-BCD=![]() S△BCD·AH=
S△BCD·AH=![]() ,即為該四面體體積的最大值.
,即為該四面體體積的最大值.


科目:高中數學 來源: 題型:
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養殖密度
(單位:千克/年)是養殖密度![]() (單位:尾/立方米)的函數.當
(單位:尾/立方米)的函數.當![]() 不超過4(尾/立方米)時,
不超過4(尾/立方米)時,![]() 的值為
的值為![]() (千克/年);當
(千克/年);當![]() 時,
時,![]() 是
是![]() 的一次函數;當
的一次函數;當![]() 達到
達到![]() (尾/立方米)時,因缺氧等原因,
(尾/立方米)時,因缺氧等原因,![]() 的值為
的值為![]() (千克/年).
(千克/年).
(1)當![]() 時,求函數
時,求函數![]() 的表達式;
的表達式;
(2)當養殖密度![]() 為多大時,魚的年生長量(單位:千克/立方米)
為多大時,魚的年生長量(單位:千克/立方米)![]() 可以達到最大,并求出最大值.
可以達到最大,并求出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著機構改革工作的深入進行,各單位要減員增效,有一家公司現有職員2a人(140<2a<420,且a為偶數),每人每年可創利b萬元.據評估,在經營條件不變的前提下,每裁員1人,則留崗職員每人每年多創利0.01b萬元,但公司需付下崗職員每人每年0.4b萬元的生活費,并且該公司正常運轉所需人數不得小于現有職員的![]() ,為獲得最大的經濟效益,該公司應裁員多少人?
,為獲得最大的經濟效益,該公司應裁員多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運
會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態度,選了某小區的100位居民調查結果統計如下:
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 80 | ||
年齡大于50歲 | 10 | ||
合計 | 70 | 100 |
(1)根據已有數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關?
(3)已知在被調查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現從這5名女性中隨機抽取3人,求至多有1位教師的概率.
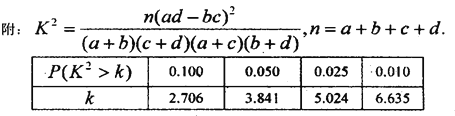
查看答案和解析>>
科目:高中數學 來源: 題型:
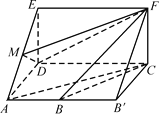
【題目】如圖,四邊形ABCD是梯形,四邊形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是線段AE上的動點.
,M是線段AE上的動點.
(1)試確定點M的位置,使AC∥平面MDF,并說明理由;
(2)在(1)的條件下,求平面MDF將幾何體ADE-BCF分成的兩部分的體積之比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考江蘇卷】已知函數![]() .設
.設![]() .
.
(1)求方程![]() 的根;
的根;
(2)若對任意![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(3)若![]() ,函數
,函數![]() 有且只有1個零點,求
有且只有1個零點,求![]() 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com