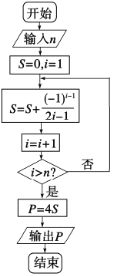
【題目】德國數學家萊布尼茲(1646年-1716年)于1674年得到了第一個關于π的級數展開式,該公式于明朝初年傳入我國.在我國科技水平業已落后的情況下,我國數學家天文學家明安圖(1692年-1765年)為提高我國的數學研究水平,從乾隆初年(1736年)開始,歷時近30年,證明了包括這個公式在內的三個公式,同時求得了展開三角函數和反三角函數的6個新級數公式,著有《割圓密率捷法》一書,為我國用級數計算π開創了先河.如圖所示的程序框圖可以用萊布尼茲“關于π的級數展開式”計算π的近似值(其中P表示π的近似值),若輸入
,則輸出的結果是( )
A.
B.
C.
D.
優生樂園系列答案
新編小學單元自測題系列答案科目：高中數學 來源： 題型：
【題目】某市垃圾處理廠的垃圾年處理量（單位：千萬噸）與資金投入量x（單位：千萬元）有如下統計數據：
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
資金投入量x（千萬元） | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾處理量y（千萬噸） | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
（1）若從統計的5年中任取2年，求這2年的垃圾處理量至少有一年不低于8.0（千萬噸）的概率；
（2）由表中數據求得線性回歸方程為
，該垃圾處理廠計劃2017年的垃圾處理量不低于9.0千萬噸，現由垃圾處理廠決策部門獲悉2017年的資金投入量約為1.8千萬元，請你預測2017年能否完成垃圾處理任務，若不能，缺口約為多少千萬噸？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且滿足
，
，設
，則以下四個命題：（1）
是等差數列；（2）
中最大項是
；（3）通項公式是
；（4）
.其中真命題的序號是______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列關于獨立性檢驗的敘述
①常用等高條形圖表示列聯表數據的頻率特征；
②獨立性檢驗依據小概率原理；
③獨立性檢驗的結果是完全正確的；
④對分類變量
與
的隨機變量
的觀測值
來說，越小，與有關系的把握程度就越大.
其中敘述正確的個數為（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】自2017年起，部分省、市陸續實施了新高考，某省采用了“
”的選科模式，即：考試除必考的語、數、外三科外，再從物理、化學、生物、歷史、地理、政治六個學科中，任意選取三科參加高考，為了調查新高考中考生的選科情況，某地區調查小組進行了一次調查，研究考生選擇化學與選擇物理是否有關.已知在調查數據中，選物理的考生與不選物理的考生人數相同，其中選物理且選化學的人數占選物理人數的
，在不選物理的考生中，選化學與不選化學的人數比為
.
（1）若在此次調查中，選物理未選化學的考生有100人，試完成下面的列聯表：
選化學 | 不選化學 | 合計（人數） | |
選物理 | |||
不選物理 | |||
合計（人數） |
（2）根據第（1）問的數據，能否有99%把握認為選擇化學與選擇物理有關？
（3）若研究得到在犯錯誤概率不超過0.01的前提下，認為選化學與選物理有關，則選物理又選化學的人數至少有多少？（單位：千人；精確到0.001）
附：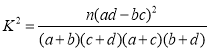
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
