
【題目】已知橢圓![]() :
:![]() (
(![]() )的左右頂點(diǎn)分別為
)的左右頂點(diǎn)分別為![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)直線![]() 不經(jīng)過點(diǎn)
不經(jīng)過點(diǎn)![]() 且與橢圓
且與橢圓![]() 交于
交于![]() ,
,![]() 兩點(diǎn),若直線
兩點(diǎn),若直線![]() 與直線
與直線![]() 的斜率之積為
的斜率之積為![]() ,證明:直線
,證明:直線![]() 過頂點(diǎn).
過頂點(diǎn).
【答案】(1) ![]() .
.
(2)見解析.
【解析】分析:第一問利用三角形的面積求得![]() 所滿足的關(guān)系,結(jié)合點(diǎn)在橢圓上,以及橢圓中
所滿足的關(guān)系,結(jié)合點(diǎn)在橢圓上,以及橢圓中![]() 的關(guān)系,求得其值,得到橢圓的方程,第二問涉及直線與橢圓相交,需要設(shè)出直線的方程,先去驗(yàn)證直線的斜率是存在的,設(shè)出方程之后,與橢圓方程聯(lián)立,消元,利用韋達(dá)定理得到其兩根和與兩根積,利用題中所給的斜率的關(guān)系,得出等量關(guān)系式,從而求得直線過定點(diǎn).
的關(guān)系,求得其值,得到橢圓的方程,第二問涉及直線與橢圓相交,需要設(shè)出直線的方程,先去驗(yàn)證直線的斜率是存在的,設(shè)出方程之后,與橢圓方程聯(lián)立,消元,利用韋達(dá)定理得到其兩根和與兩根積,利用題中所給的斜率的關(guān)系,得出等量關(guān)系式,從而求得直線過定點(diǎn).
詳解:(1)由題意可設(shè)橢圓的半焦距為![]() ,
,
由題意得:
所以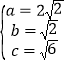
所以橢圓![]() 的方程為:
的方程為:![]()
(2)![]() 當(dāng)直線
當(dāng)直線![]() 的斜率不存在時(shí),可設(shè)其方程為
的斜率不存在時(shí),可設(shè)其方程為![]() 且
且![]() ),
),
不妨設(shè)![]() ,
,![]() 且
且![]()
故![]() 把
把![]() 代換化簡得:
代換化簡得:![]() ,
,![]() 不合題意
不合題意
![]() 設(shè)直線
設(shè)直線![]() 的方程為
的方程為![]() ,
,![]() ,
,![]()
聯(lián)立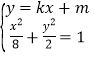
![]()
![]() ,
,
由![]() ,
,![]() 是上方程的兩個(gè)根可知:
是上方程的兩個(gè)根可知: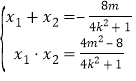
由![]() ,
,![]()
![]()
化簡整理得:![]()
即![]()
故![]() 或
或![]() (舍去,因?yàn)榇藭r(shí)直線經(jīng)過點(diǎn)
(舍去,因?yàn)榇藭r(shí)直線經(jīng)過點(diǎn)![]() )
)
把![]() 代入
代入![]() 得
得![]()
![]()
所以直線方程為![]() (
(![]() ),恒過點(diǎn)
),恒過點(diǎn)![]()


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() ,點(diǎn)
,點(diǎn)![]() 是曲線
是曲線![]() 上的動(dòng)點(diǎn).點(diǎn)
上的動(dòng)點(diǎn).點(diǎn)![]() 滿足
滿足![]() (
(![]() 為極點(diǎn)).設(shè)點(diǎn)
為極點(diǎn)).設(shè)點(diǎn)![]() 的軌跡為曲線
的軌跡為曲線![]() .以極點(diǎn)
.以極點(diǎn)![]() 為原點(diǎn),極軸為
為原點(diǎn),極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系
軸的正半軸建立平面直角坐標(biāo)系![]() ,已知直線
,已知直線![]() 的參數(shù)方程是
的參數(shù)方程是![]() ,(
,(![]() 為參數(shù)).
為參數(shù)).
(1)求曲線![]() 的直角坐標(biāo)方程與直線
的直角坐標(biāo)方程與直線![]() 的普通方程;
的普通方程;
(2)設(shè)直線![]() 交兩坐標(biāo)軸于
交兩坐標(biāo)軸于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若函數(shù)![]() 有兩個(gè)極值點(diǎn)
有兩個(gè)極值點(diǎn)![]() 且
且![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,ABCD是一塊邊長為7米的正方形鐵皮,其中ATN是一半徑為6米的扇形,已經(jīng)被腐蝕不能使用,其余部分完好可利用.工人師傅想在未被腐蝕部分截下一個(gè)有邊落在BC與CD上的長方形鐵皮![]() ,其中P是弧TN上一點(diǎn).設(shè)
,其中P是弧TN上一點(diǎn).設(shè)![]() ,長方形
,長方形![]() 的面積為S平方米.
的面積為S平方米.
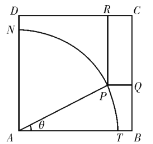
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某桶裝水經(jīng)營部每天的房租,人員工資等固定成本為200元,每桶水的進(jìn)價(jià)是5元,銷售價(jià)![]() (元)與日均銷售量
(元)與日均銷售量![]() (桶)的關(guān)系如下表,為了收費(fèi)方便,經(jīng)營部將銷售價(jià)定為整數(shù),并保持經(jīng)營部每天盈利.
(桶)的關(guān)系如下表,為了收費(fèi)方便,經(jīng)營部將銷售價(jià)定為整數(shù),并保持經(jīng)營部每天盈利.
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | … |
| 480 | 440 | 400 | 360 | 320 | 280 | 240 | … |
(1)寫出![]() 的值,并解釋其實(shí)際意義;
的值,并解釋其實(shí)際意義;
(2)求![]() 表達(dá)式,并求其定義域;
表達(dá)式,并求其定義域;
(3)求經(jīng)營部利潤表達(dá)式![]() ,請(qǐng)問經(jīng)營部怎樣定價(jià)才能獲得最大利潤?
,請(qǐng)問經(jīng)營部怎樣定價(jià)才能獲得最大利潤?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,已知曲線
中,已知曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù))。曲線
為參數(shù))。曲線![]() 的參數(shù)方程為
的參數(shù)方程為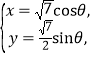 (
(![]() 為參數(shù)),在以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),在以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸正半軸為極軸建立極坐標(biāo)系.
軸正半軸為極軸建立極坐標(biāo)系.
(1)求曲線![]() ,
,![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)在極坐標(biāo)系中,射線![]() 與曲線
與曲線![]() 交于點(diǎn)
交于點(diǎn)![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于點(diǎn)
交于點(diǎn)![]() ,求
,求![]() 的面積(其中
的面積(其中![]() 為坐標(biāo)原點(diǎn)).
為坐標(biāo)原點(diǎn)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
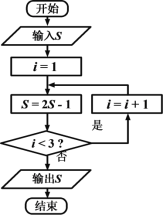
【題目】《算法統(tǒng)宗》是中國古代數(shù)學(xué)名著,由明代數(shù)學(xué)家程大位所著,該作完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉(zhuǎn)變,該作中有題為“李白沽酒”“李白街上走,提壺去買酒。遇店加一倍,見花喝一斗,三遇店和花,喝光壺中酒。借問此壺中,原有多少酒?”,如圖為該問題的程序框圖,若輸出的![]() 值為0,則開始輸入的
值為0,則開始輸入的![]() 值為( )
值為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com