
【題目】已知函數 ![]() 的兩條相鄰對稱軸間的距離為
的兩條相鄰對稱軸間的距離為 ![]() ,把f(x)的圖象向右平移
,把f(x)的圖象向右平移 ![]() 個單位得到函數g(x)的圖象,且g(x)為偶函數,則f(x)的單調遞增區間為( )
個單位得到函數g(x)的圖象,且g(x)為偶函數,則f(x)的單調遞增區間為( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵函數f(x)的兩條相鄰對稱軸間的距離為 ![]() , ∴
, ∴ ![]() =
= ![]() ,即周期T=
,即周期T= ![]() ,則ω=2,
,則ω=2,
此時f(x)=2sin(2x+φ),
把f(x)的圖象向右平移 ![]() 個單位得到函數g(x)的圖象,
個單位得到函數g(x)的圖象,
則g(x)=2sin[2(x﹣ ![]() )+φ]=2sin(2x+φ﹣
)+φ]=2sin(2x+φ﹣ ![]() ),
),
∵g(x)為偶函數,
∴φ﹣ ![]() =
= ![]() +kπ,
+kπ,
則φ= ![]() +kπ,k∈Z,
+kπ,k∈Z,
∵|φ|< ![]() ,
,
∴當k=﹣1時,φ= ![]() ﹣π=﹣
﹣π=﹣ ![]() ,
,
則f(x)=2sin(2x﹣ ![]() ),
),
由2kπ﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,
,k∈Z,
得2kπ﹣ ![]() ≤2x≤2kπ+
≤2x≤2kπ+ ![]() ,
,
即kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
即函數的單調遞增區間為[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z,
],k∈Z,
故選:C.
【考點精析】通過靈活運用正弦函數的單調性和函數y=Asin(ωx+φ)的圖象變換,掌握正弦函數的單調性:在![]()
![]() 上是增函數;在
上是增函數;在![]()
![]() 上是減函數;圖象上所有點向左(右)平移
上是減函數;圖象上所有點向左(右)平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的橫坐標伸長(縮短)到原來的
的圖象上所有點的橫坐標伸長(縮短)到原來的![]() 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數![]() 的圖象;再將函數
的圖象;再將函數![]() 的圖象上所有點的縱坐標伸長(縮短)到原來的
的圖象上所有點的縱坐標伸長(縮短)到原來的![]() 倍(橫坐標不變),得到函數
倍(橫坐標不變),得到函數![]() 的圖象即可以解答此題.
的圖象即可以解答此題.


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】下表是一位母親給兒子作的成長記錄:
年齡/周歲 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.1 |
根據以上樣本數據,她建立了身高 ![]() (cm)與年齡x(周歲)的線性回歸方程為
(cm)與年齡x(周歲)的線性回歸方程為 ![]() ,給出下列結論:
,給出下列結論:
①y與x具有正的線性相關關系;
②回歸直線過樣本的中心點(42,117.1);
③兒子10歲時的身高是 ![]() cm;
cm;
④兒子年齡增加1周歲,身高約增加 ![]() cm.
cm.
其中,正確結論的個數是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的前n項和為Sn=a2n+b,且a1=3.
(1)求a、b的值及數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和Tn .
,求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小朋友按如下規則練習數數,![]() 大拇指,
大拇指,![]() 食指,
食指,![]() 中指,
中指,![]() 無名指,
無名指,![]() 小指,
小指,![]() 無名指,
無名指,![]() 中指,
中指,![]() 食指,
食指,![]() 大拇指,
大拇指,![]() 食指,
食指,![]() ,一直數到
,一直數到![]() 時,對應的指頭是( )
時,對應的指頭是( )

A. 小指 B. 中指 C. 食指 D. 無名指
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》有如下問題:有上禾三秉(古代容量單位),中禾二秉,下禾一秉,實三十九斗;上禾二秉,中禾三秉,下禾一秉,實三十四斗;上禾一秉,中禾二秉,下禾三秉,實二十六斗.問上、中、下禾一秉各幾何?依上文:設上、中、下禾一秉分別為x斗、y斗、z斗,設計如圖所示的程序框圖,則輸出的x,y,z的值分別為( ) 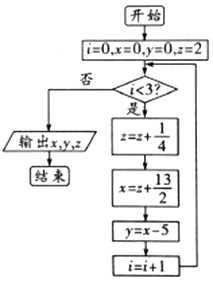
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() 的離心率為
的離心率為 ![]() ,且它的一個焦點
,且它的一個焦點 ![]() 的坐標為
的坐標為 ![]() .
.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)設過焦點 ![]() 的直線與橢圓相交于
的直線與橢圓相交于 ![]() 兩點,
兩點, ![]() 是橢圓上不同于
是橢圓上不同于 ![]() 的動點,試求
的動點,試求 ![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面程序框圖中,若輸入互不相等的三個正實數a,b,c(abc≠0),要求判斷△ABC的形狀,則空白的判斷框應填入( ) 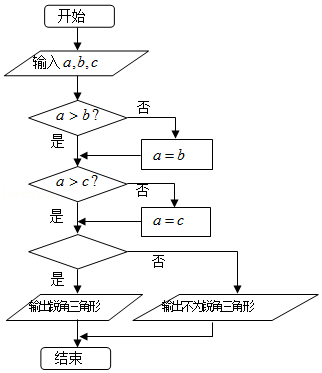
A.a2+b2>c2?
B.a2+c2>b2?
C.b2+c2>a2?
D.b2+a2=c2?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com