
【題目】已知數(shù)列![]() 是公比大于
是公比大于![]() 的等比數(shù)列,
的等比數(shù)列,![]() 為數(shù)列
為數(shù)列![]() 的前
的前![]() 項(xiàng)和,
項(xiàng)和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數(shù)列.數(shù)列
成等差數(shù)列.數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,
,![]() 滿(mǎn)足
滿(mǎn)足![]() ,且
,且![]() ,
,
(1)求數(shù)列![]() 和
和![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)令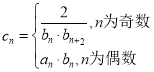 ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ;
;
(3)將數(shù)列![]() ,
,![]() 的項(xiàng)按照“當(dāng)
的項(xiàng)按照“當(dāng)![]() 為奇數(shù)時(shí),
為奇數(shù)時(shí),![]() 放在前面;當(dāng)
放在前面;當(dāng)![]() 為偶數(shù)時(shí),
為偶數(shù)時(shí),![]() 放在前面”的要求進(jìn)行排列,得到一個(gè)新的數(shù)列:
放在前面”的要求進(jìn)行排列,得到一個(gè)新的數(shù)列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求這個(gè)新數(shù)列的前
,求這個(gè)新數(shù)列的前![]() 項(xiàng)和
項(xiàng)和![]() .
.
【答案】(1)![]() ,
,![]()
![]() (2)
(2)![]() (3)
(3)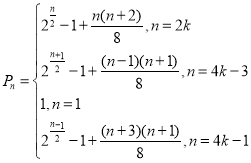
【解析】
(1)設(shè)等比數(shù)列![]() 的公比為
的公比為![]() ,依題意得到關(guān)于
,依題意得到關(guān)于![]() 、
、![]() 的方程組解得,由
的方程組解得,由![]() ,可知
,可知![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公差為
,公差為![]() 的等差數(shù)列,求出
的等差數(shù)列,求出![]() 的通項(xiàng)公式,即可求出
的通項(xiàng)公式,即可求出![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)利用分組求和,錯(cuò)位相減,裂項(xiàng)相消求其前![]() 項(xiàng)和為
項(xiàng)和為![]() ;
;
(3)分![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,三種情況討論可得;
,三種情況討論可得;
解:(1)設(shè)等比數(shù)列![]() 的公比為
的公比為![]() ,
,
由已知,得 ,
,
即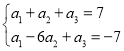 ,也即
,也即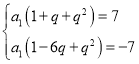
解得![]()
故數(shù)列![]() 的通項(xiàng)為
的通項(xiàng)為![]() .
.
![]() ,
,
![]() 是首項(xiàng)為
是首項(xiàng)為![]() ,公差為
,公差為![]() 的等差數(shù)列,
的等差數(shù)列,
![]() ,
,
![]()
![]()
![]()
![]()
(2)
其中![]()
![]()
令![]()
則![]() ①
①
![]() ②
②
①減②得![]()
![]()
![]()
![]() ,
,
∴![]()
![]()
![]()
![]()
(3)數(shù)列![]() 前
前![]() 項(xiàng)和
項(xiàng)和![]() ,數(shù)列
,數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() ;
;
①當(dāng)![]()
![]() ,
,![]()
②當(dāng)![]()
![]()
⑴當(dāng)![]() 時(shí),
時(shí),![]()
⑵當(dāng)![]() 時(shí),
時(shí),
![]()
③當(dāng)![]()
![]()
![]()
綜上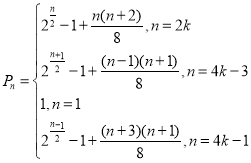



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以該直角坐標(biāo)系的原點(diǎn)
為參數(shù)),以該直角坐標(biāo)系的原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn),![]() 軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點(diǎn),交曲線
兩點(diǎn),交曲線![]() 于
于![]() ,
,![]() 兩點(diǎn),求
兩點(diǎn),求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,射線![]() 的普通方程為
的普通方程為![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線
為參數(shù)).以O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫(xiě)出![]() 與
與![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)設(shè)![]() 與
與![]() 的交點(diǎn)為P(點(diǎn)P不為極點(diǎn)),
的交點(diǎn)為P(點(diǎn)P不為極點(diǎn)),![]() 與
與![]() 的交點(diǎn)為Q,當(dāng)
的交點(diǎn)為Q,當(dāng)![]() 在
在![]() 上變化時(shí),求
上變化時(shí),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在正方體![]() 中,
中,![]() 、
、![]() 分別是棱
分別是棱![]() 、
、![]() 的中點(diǎn),
的中點(diǎn),![]() 、
、![]() 分別是線段
分別是線段![]() 與
與![]() 上的點(diǎn),則與平面
上的點(diǎn),則與平面![]() 平行的直線
平行的直線![]() 有( )
有( )
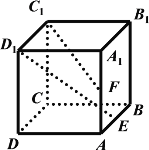
A.0條B.1條C.2條D.無(wú)數(shù)條
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】有次水下考古活動(dòng)中,潛水員需潛入水深為30米的水底進(jìn)行作業(yè),其用氧量包含以下三個(gè)方面:①下潛時(shí),平均速度為每分鐘![]() 米,每分鐘的用氧量為
米,每分鐘的用氧量為![]() 升;②水底作業(yè)需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時(shí),速度為每分鐘
升;②水底作業(yè)需要10分鐘,每分鐘的用氧量為0.3升;③返回水面時(shí),速度為每分鐘![]() 米,每分鐘用氧量為0.2升;設(shè)潛水員在此次考古活動(dòng)中的總用氧量為
米,每分鐘用氧量為0.2升;設(shè)潛水員在此次考古活動(dòng)中的總用氧量為![]() 升;
升;
(1)將![]() 表示為
表示為![]() 的函數(shù);
的函數(shù);
(2)若![]() ,求總用氧量
,求總用氧量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=ax+blnx(a,b∈R)在點(diǎn)(1,f(1))處的切線方程為y![]() x﹣1.
x﹣1.
(1)求ab的值;
(2)當(dāng)x>1時(shí),f(x)![]() 0恒成立,求實(shí)數(shù)k的取值范圍;
0恒成立,求實(shí)數(shù)k的取值范圍;
(3)設(shè)g(x)=ex![]() x,求證:對(duì)于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
x,求證:對(duì)于x∈(0,+∞),g(x)﹣f(x)>2恒成立.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】對(duì)于定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若存在正常數(shù)
,若存在正常數(shù)![]() 、
、![]() ,使得
,使得![]() 對(duì)一切
對(duì)一切![]() 均成立,則稱(chēng)
均成立,則稱(chēng)![]() 是“控制增長(zhǎng)函數(shù)”,在以下四個(gè)函數(shù)中:①
是“控制增長(zhǎng)函數(shù)”,在以下四個(gè)函數(shù)中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增長(zhǎng)函數(shù)”的有( )
.是“控制增長(zhǎng)函數(shù)”的有( )
A.②③B.③④C.②③④D.①②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 且在
且在![]() 上的最大值為
上的最大值為![]() ,
,
(1)求函數(shù)f(x)的解析式;
(2)判斷函數(shù)f(x)在(0,π)內(nèi)的零點(diǎn)個(gè)數(shù),并加以證明
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】追求人類(lèi)與生存環(huán)境的和諧發(fā)展是中國(guó)特色社會(huì)主義生態(tài)文明的價(jià)值取向.為了改善空氣質(zhì)量,某城市環(huán)保局隨機(jī)抽取了一年內(nèi)100天的空氣質(zhì)量指數(shù)(![]() )的檢測(cè)數(shù)據(jù),結(jié)果統(tǒng)計(jì)如下:
)的檢測(cè)數(shù)據(jù),結(jié)果統(tǒng)計(jì)如下:
|
|
|
|
|
|
|
空氣質(zhì)量 | 優(yōu) | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴(yán)重污染 |
天數(shù) | 6 | 14 | 18 | 27 | 25 | 10 |
(1)從空氣質(zhì)量指數(shù)屬于![]() ,
,![]() 的天數(shù)中任取3天,求這3天中空氣質(zhì)量至少有2天為優(yōu)的概率;
的天數(shù)中任取3天,求這3天中空氣質(zhì)量至少有2天為優(yōu)的概率;
(2)已知某企業(yè)每天的經(jīng)濟(jì)損失![]() (單位:元)與空氣質(zhì)量指數(shù)
(單位:元)與空氣質(zhì)量指數(shù)![]() 的關(guān)系式為
的關(guān)系式為 ,試估計(jì)該企業(yè)一個(gè)月(按30天計(jì)算)的經(jīng)濟(jì)損失的數(shù)學(xué)期望.
,試估計(jì)該企業(yè)一個(gè)月(按30天計(jì)算)的經(jīng)濟(jì)損失的數(shù)學(xué)期望.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com