
【題目】如果一個實數數列{an}滿足條件: ![]() (d為常數,n∈N*),則稱這一數列“偽等差數列”,d稱為“偽公差”.給出下列關于某個偽等差數列{an}的結論:①對于任意的首項a1 , 若d<0,則這一數列必為有窮數列;②當d>0,a1>0時,這一數列必為單調遞增數列;③這一數列可以是一個周期數列;④若這一數列的首項為1,偽公差為3,-
(d為常數,n∈N*),則稱這一數列“偽等差數列”,d稱為“偽公差”.給出下列關于某個偽等差數列{an}的結論:①對于任意的首項a1 , 若d<0,則這一數列必為有窮數列;②當d>0,a1>0時,這一數列必為單調遞增數列;③這一數列可以是一個周期數列;④若這一數列的首項為1,偽公差為3,- ![]() 可以是這一數列中的一項;n∈N*⑤若這一數列的首項為0,第三項為﹣1,則這一數列的偽公差可以是
可以是這一數列中的一項;n∈N*⑤若這一數列的首項為0,第三項為﹣1,則這一數列的偽公差可以是 ![]() .其中正確的結論是 .
.其中正確的結論是 .
【答案】③④
【解析】解:①當a1= ![]() 、d=﹣
、d=﹣ ![]() 、an>0時,
、an>0時,
依題意,an= ![]() ,故不正確;
,故不正確;
②當d>0,a1>0時,
∵an+1=± ![]() ,
,
∴這一數列不是單調遞增數列,故不正確;
③易知當偽公差d=0、an=1時,這一數列是周期數列,故正確;
④∵a1=1,d=3,
∴a2=± ![]() =±2,
=±2,
∴當a2=2時a3=± ![]()
![]() ,故正確;
,故正確;
⑤∵a1=0,a3=﹣1,
∴ ![]() =a1+d=d,
=a1+d=d,
∴d≥0,
而 ![]() <0,故不正確;
<0,故不正確;
綜上所述:③④正確,①②⑤不正確,
所以答案是:③④.
【考點精析】本題主要考查了數列的通項公式的相關知識點,需要掌握如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式才能正確解答此題.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
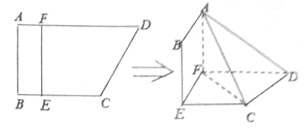
【題目】如圖,四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別在
分別在![]() 上,
上, ![]() ,現將四邊形
,現將四邊形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)當![]() ,是否在折疊后的
,是否在折疊后的![]() 上存在一點
上存在一點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 點位置,若不存在,說明理由;
點位置,若不存在,說明理由;
(2)設![]() ,問當
,問當![]() 為何值時,三棱錐
為何值時,三棱錐![]() 的體積有最大值?并求出這個最大值.
的體積有最大值?并求出這個最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為倡導全體學生為特困學生捐款,舉行“一元錢,一片心,誠信用水”活動,學生在購水處每領取一瓶礦泉水,便自覺向捐款箱中至少投入一元錢.現統計了連續5天的售出和收益情況,如表:
售出水量x(單位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(單位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y關于x的線性回歸方程;
(2)預測售出8箱水的收益是多少元?
附:回歸直線的最小二乘法估計公式分別為:![]() =
=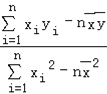 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班同學利用國慶節進行社會實踐,對[25,55]歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖:
人進行了一次生活習慣是否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得到如下統計表和各年齡段人數頻率分布直方圖:
組數 | 分組 | 低碳族的人數 | 占本組的頻率 |
第一組 | [25,30) | 120 | 0.6 |
第二組 | [30,35) | 195 |
|
第三組 | [35,40) | 100 | 0.5 |
第四組 | [40,45) |
| 0.4 |
第五組 | [45,50) | 30 | 0.3 |
第六組 | [50,55] | 15 | 0.3 |
(1)補全頻率分布直方圖并求![]() 的值;
的值;
(2)從年齡段在[40,50)的“低碳族”中采用分層抽樣法抽取6人參加戶外低碳體驗活動,其中選取2人作為領隊,求選取的2名領隊中恰有1人年齡在[40,45)歲的概率.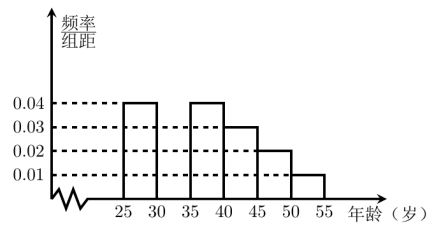
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出![]() 該產品獲利潤500元,未售出的產品,每
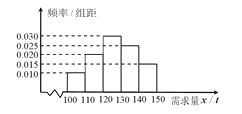
該產品獲利潤500元,未售出的產品,每![]() 虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了
虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該農產品.以
該農產品.以![]() (
(![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量, ![]() (單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(Ⅰ)將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)根據直方圖估計利潤![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲,乙兩臺機床同時生產一種零件,其質量按測試指標劃分:指標大于或等于95為正品,小于95為次品,現隨機抽取這兩臺車床生產的零件各100件進行檢測,檢測結果統計如下:
測試指標 |
|
|
|
|
|
機床甲 | 8 | 12 | 40 | 32 | 8 |
機床乙 | 7 | 18 | 40 | 29 | 6 |
(1)試分別估計甲機床、乙機床生產的零件為正品的概率;
(2)甲機床生產一件零件,若是正品可盈利160元,次品則虧損20元;乙機床生產一件零件,若是正品可盈利200元,次品則虧損40元,在(1)的前提下,現需生產這種零件2件,以獲得利潤的期望值為決策依據,應該如何安排生產最佳?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a1+3a2=1,a32=9a2a6 ,
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+…+log3an , 求數列{ ![]() }的前n項和.
}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中, ![]() ,
, ![]() 為邊
為邊![]() 的中點,將
的中點,將![]() 沿直線
沿直線![]() 翻轉成
翻轉成![]() .若
.若![]() 為線段
為線段![]() 的中點,則在
的中點,則在![]() 翻折過程中:
翻折過程中:

①![]() 是定值;②點
是定值;②點![]() 在某個球面上運動;
在某個球面上運動;
③存在某個位置,使![]() ;④存在某個位置,使
;④存在某個位置,使![]() 平面
平面![]() .
.
其中正確的命題是_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com