
【題目】如圖所示,在四邊形ABCD中,AC=CD=![]() AB=1,
AB=1, ![]() ,sin∠BCD=
,sin∠BCD=![]() .
.
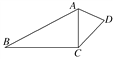
(1)求BC邊的長;
(2)求四邊形ABCD的面積.
【答案】(1) ![]() (2)
(2) ![]()
【解析】 試題分析:(1)先根據(jù)向量數(shù)量積求∠BAC,再根據(jù)余弦定理求BC邊的長;(2)四邊形ABCD的面積等于兩個(gè)三角形面積之和,而△ABC為直角三角形,可得其面積;根據(jù)∠BCD=∠ACB+∠ACD=90°+∠ACD,所以先由sin∠BCD=![]() 求sin∠ACD,再根據(jù)三角形面積公式求S△ACD,最后相加得四邊形ABCD的面積
求sin∠ACD,再根據(jù)三角形面積公式求S△ACD,最后相加得四邊形ABCD的面積
試題解析:(1)∵AC=CD=![]() AB=1,∴
AB=1,∴![]() =2cos∠BAC=1.
=2cos∠BAC=1.
∴cos∠BAC=![]() ,∴∠BAC=60°.
,∴∠BAC=60°.
在△ABC中,由余弦定理,有
BC2=AB2+AC2-2AB·AC·cos∠BAC=22+12-2×2×1×![]() =3,∴BC=
=3,∴BC=![]() .
.
(2)由(1)知,在△ABC中,有AB2=BC2+AC2.∴△ABC為直角三角形,且∠ACB=90°.
∴S△ABC=![]() BC·AC=
BC·AC=![]()
又∠BCD=∠ACB+∠ACD=90°+∠ACD,sin∠BCD=,∴cos∠ACD=.
從而sin∠ACD=![]() .
.
∴S△ACD=![]() AC·CD·sin∠ACD=
AC·CD·sin∠ACD=![]() ×1×1×
×1×1×![]() =.
=.
∴S四邊形ABCD=S△ABC+S△ACD=+=![]() .
.


 作業(yè)輔導(dǎo)系列答案
作業(yè)輔導(dǎo)系列答案 同步學(xué)典一課多練系列答案
同步學(xué)典一課多練系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面是以
中,底面是以![]() 為中心的菱形,
為中心的菱形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() 為
為![]() 上一點(diǎn),且
上一點(diǎn),且![]() .
.
(1)證明: ![]() 平面
平面![]() ;
;
(2)若![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
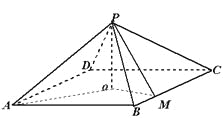
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在銳角三角形中,邊a、b是方程x2﹣2 ![]() x+2=0的兩根,角A、B滿足:2sin(A+B)﹣
x+2=0的兩根,角A、B滿足:2sin(A+B)﹣ ![]() =0,求角C的度數(shù),邊c的長度及△ABC的面積.
=0,求角C的度數(shù),邊c的長度及△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}的前n項(xiàng)和為Sn , 且滿足Sn=2an﹣2.若數(shù)列{bn}滿足bn=10﹣log2an , 則是數(shù)列{bn}的前n項(xiàng)和取最大值時(shí)n的值為( )
A.8
B.10
C.8或9
D.9或10
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市為了了解今年高中畢業(yè)生的體能狀況,從某校高中畢業(yè)班中抽取一個(gè)班進(jìn)行鉛球測試,成績在8.0米(精確到0.1米)以上的為合格.?dāng)?shù)據(jù)分成6組畫出頻率分布直方圖的一部分(如圖),已知從左到右前5個(gè)小組的頻率分別為0.04,0.10,0.14,0.28,0.30 .第6小組的頻數(shù)是7.
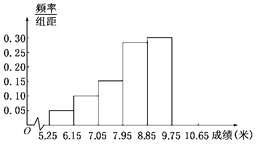
(I)求這次鉛球測試成績合格的人數(shù);
(II)若參加測試的學(xué)生中9人成績優(yōu)秀,現(xiàn)要從成績優(yōu)秀的學(xué)生中,隨機(jī)選出2人參加“畢業(yè)運(yùn)動(dòng)會(huì)”,已知學(xué)生![]() 、
、![]() 的成績均為優(yōu)秀,求兩人
的成績均為優(yōu)秀,求兩人![]() 、
、![]() 至少有1人入選的概率.
至少有1人入選的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,在四邊形ABCD中,AB⊥DA,CE= ![]() ,∠ADC=
,∠ADC= ![]() ;E為AD邊上一點(diǎn),DE=1,EA=2,∠BEC=
;E為AD邊上一點(diǎn),DE=1,EA=2,∠BEC= ![]()
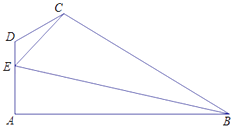
(1)求sin∠CED的值;
(2)求BE的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某食品店為了了解氣溫對銷售量的影響,隨機(jī)記錄了該店1月份中5天的日銷售量![]() (單位:千克)與該地當(dāng)日最低氣溫
(單位:千克)與該地當(dāng)日最低氣溫![]() (單位:
(單位: ![]() )的數(shù)據(jù),如下表:
)的數(shù)據(jù),如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 與
與![]() 的回歸方程
的回歸方程![]() ;
;
(2)判斷![]() 與
與![]() 之間是正相關(guān)還是負(fù)相關(guān);若該地1月份某天的最低氣溫為
之間是正相關(guān)還是負(fù)相關(guān);若該地1月份某天的最低氣溫為![]() ,請用所求回歸方程預(yù)測該店當(dāng)日的銷售量;
,請用所求回歸方程預(yù)測該店當(dāng)日的銷售量;
(3)設(shè)該地1月份的日最低氣溫![]() ~
~![]() ,其中
,其中![]() 近似為樣本平均數(shù)
近似為樣本平均數(shù)![]() ,
, ![]() 近似為樣本方差
近似為樣本方差![]() ,求
,求![]() .
.
附:①回歸方程![]() 中,
中, 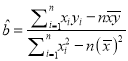 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,則
,則![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“累積凈化量![]() ”是空氣凈化器質(zhì)量的一個(gè)重要衡量指標(biāo),它是指空氣凈化從開始使用到凈化效率為50%時(shí)對顆粒物的累積凈化量,以克表示,根據(jù)
”是空氣凈化器質(zhì)量的一個(gè)重要衡量指標(biāo),它是指空氣凈化從開始使用到凈化效率為50%時(shí)對顆粒物的累積凈化量,以克表示,根據(jù)![]() 《空氣凈化器》國家標(biāo)準(zhǔn),對空氣凈化器的累計(jì)凈化量
《空氣凈化器》國家標(biāo)準(zhǔn),對空氣凈化器的累計(jì)凈化量![]() 有如下等級(jí)劃分:
有如下等級(jí)劃分:
累積凈化量(克) |
|
|
| 12以上 |
等級(jí) |
|
|
|
|
為了了解一批空氣凈化器(共5000臺(tái))的質(zhì)量,隨機(jī)抽取![]() 臺(tái)機(jī)器作為樣本進(jìn)行估計(jì),已知這
臺(tái)機(jī)器作為樣本進(jìn)行估計(jì),已知這![]() 臺(tái)機(jī)器的累積凈化量都分布在區(qū)間
臺(tái)機(jī)器的累積凈化量都分布在區(qū)間![]() 中,按照
中,按照![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 均勻分組,其中累積凈化量在
均勻分組,其中累積凈化量在![]() 的所有數(shù)據(jù)有:4.5,4.6,5.2,5.3,5.7和5.9,并繪制了頻率分布直方圖,如圖所示:
的所有數(shù)據(jù)有:4.5,4.6,5.2,5.3,5.7和5.9,并繪制了頻率分布直方圖,如圖所示:
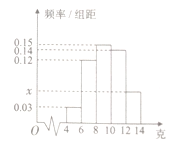
(1)求![]() 的值及頻率分布直方圖中
的值及頻率分布直方圖中![]() 的值;
的值;
(2)以樣本估計(jì)總體,試估計(jì)這批空氣凈化器(共5000臺(tái))中等級(jí)為![]() 的空氣凈化器有多少臺(tái)?
的空氣凈化器有多少臺(tái)?
(3)從累積凈化量在![]() 的樣本中隨機(jī)抽取2臺(tái),求恰好有1臺(tái)等級(jí)為
的樣本中隨機(jī)抽取2臺(tái),求恰好有1臺(tái)等級(jí)為![]() 的概率.
的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com