
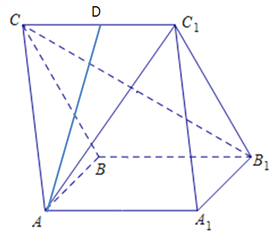
【題目】如圖所示,在三棱柱![]() 中,
中,![]() 為正方形,
為正方形,![]() 為菱形,
為菱形,![]() .
.
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 中點,
中點,![]() 是二面角
是二面角![]() 的平面角,求直線
的平面角,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)先根據(jù)平面幾何知識證明![]() 從而可得
從而可得![]() 面
面![]() ,可得
,可得![]() ,進而得
,進而得![]() 平面
平面![]() ,再由面面垂直的判定定理可得結(jié)論;(2)建立空間坐標系,求出平面的法向量,利用向量法求解即可.
,再由面面垂直的判定定理可得結(jié)論;(2)建立空間坐標系,求出平面的法向量,利用向量法求解即可.
試題解析:(1)證明:連接![]() ,因為
,因為![]() 為菱形,所以
為菱形,所以![]() ,又
,又![]() ,
,
![]() ,所以
,所以![]() 面
面![]() .
.
故![]() .
.
因為![]() ,且
,且![]() ,所以
,所以![]() 面
面![]() .
.
而![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)因為![]() 是二面角
是二面角![]() 的平面角,所以
的平面角,所以![]() ,又
,又![]() 是
是![]() 中點,
中點,
所以![]() ,所以
,所以![]() 為等邊三角形.
為等邊三角形.
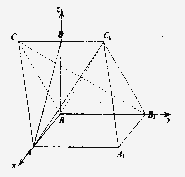
如圖所示,分別以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
不妨設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
設(shè)![]() 是平面
是平面![]() 的一個法向量,則
的一個法向量,則
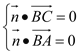 ,即
,即![]() ,
,
取![]() 得
得![]() .
.
所以
![]() ,
,
所以直線![]() 與平面
與平面![]() 所成的余弦值為
所成的余弦值為![]() .
.
【方法點晴】本題主要考查利用求二面角,面面垂直的判定定理,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當?shù)目臻g直角坐標系;(2)寫出相應(yīng)點的坐標,求出相應(yīng)直線的方向向量;(3)設(shè)出相應(yīng)平面的法向量,利用兩直線垂直數(shù)量積為零列出方程組求出法向量;(4)將空間位置關(guān)系轉(zhuǎn)化為向量關(guān)系;(5)根據(jù)定理結(jié)論求出相應(yīng)的角和距離.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)是定義在R上的奇函數(shù),當x≥0時,f(x)=(|x﹣a2|+|x﹣2a2|﹣3a2),若對于任意x∈R,都有f(x﹣2)≤f(x),則實數(shù)a的取值范圍是( )
A.[﹣ ![]() ,
, ![]() ]
]
B.[﹣ ![]() ,
, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知四棱錐S﹣ABCD,底面ABCD為菱形,SA⊥平面ABCD,∠ADC=60°,E,F(xiàn)分別是SC,BC的中點. 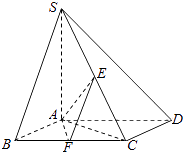
(1)證明:SD⊥AF;
(2)若AB=2,SA=4,求二面角F﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ),數(shù)列
),數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,點
,點![]() 在
在![]() 圖象上,且
圖象上,且![]() 的最小值為
的最小值為![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)數(shù)列![]() 滿足
滿足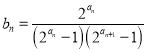 ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列結(jié)論正確的個數(shù)是( )
①命題“所有的四邊形都是矩形”是特稱命題;
②命題“x∈R,x2+2<0”是全稱命題;
③若p:x∈R,x2+4x+4≤0,則q:x∈R,x2+4x+4≤0是全稱命題.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
, ![]() ,
, ![]() ),
),![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(Ⅰ)當![]() ,
, ![]() 時,求函數(shù)
時,求函數(shù)![]() 的零點個數(shù);
的零點個數(shù);
(Ⅱ)若![]() ,求
,求![]() 在
在![]() 上的最大值.
上的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是(只填正確說法序號)
①若集合A={y|y=x﹣1},B={y|y=x2﹣1},則A∩B={(0,﹣1),(1,0)};
② ![]() 是函數(shù)解析式;
是函數(shù)解析式;
③ ![]() 是非奇非偶函數(shù);
是非奇非偶函數(shù);
④設(shè)二次函數(shù)f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),則f(x1+x2)=c.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)命題p:f(x)= ![]() 在區(qū)間(1,+∞)上是減函數(shù);命題q;x1x2是方程x2﹣ax﹣2=0的兩個實根,不等式m2+5m﹣3≥|x1﹣x2|對任意實數(shù)α∈[﹣1,1]恒成立;若¬p∧q為真,試求實數(shù)m的取值范圍.
在區(qū)間(1,+∞)上是減函數(shù);命題q;x1x2是方程x2﹣ax﹣2=0的兩個實根,不等式m2+5m﹣3≥|x1﹣x2|對任意實數(shù)α∈[﹣1,1]恒成立;若¬p∧q為真,試求實數(shù)m的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com