
【題目】某商場為提高服務質量,隨機調查了60名男顧客和80名女顧客,每位顧客均對該商場的服務給出滿意或不滿意的評價,得到下面不完整的列聯表:
滿意 | 不滿意 | 合計 | |
男顧客 | 50 | ||
女顧客 | 50 | ||
合計 |
(1)根據已知條件將列聯表補充完整;
(2)能否有![]() 的把握認為男、女顧客對該商場服務的評價有差異?
的把握認為男、女顧客對該商場服務的評價有差異?
附: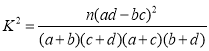
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
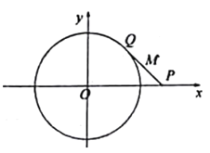
【題目】已知![]() 是
是![]() 軸上的動點(異于原點
軸上的動點(異于原點![]() ),點
),點![]() 在圓
在圓![]() 上,且
上,且![]() .設線段
.設線段![]() 的中點為
的中點為![]() ,當點
,當點![]() 移動時,記點
移動時,記點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)當直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,且點
,且點![]() 在第一象限.
在第一象限.
(ⅰ)求直線![]() 的斜率;
的斜率;
(ⅱ)直線![]() 平行
平行![]() ,交曲線
,交曲線![]() 于不同的兩點
于不同的兩點![]() 、
、![]() .線段
.線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() 、
、![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】區塊鏈技術被認為是繼蒸汽機、電力、互聯網之后,下一代顛覆性的核心技術區塊鏈作為構造信任的機器,將可能徹底改變整個人類社會價值傳遞的方式,2015年至2019年五年期間,中國的區塊鏈企業數量逐年增長,居世界前列現收集我國近5年區塊鏈企業總數量相關數據,如表
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
編號 | 1 | 2 | 3 | 4 | 5 |
企業總數量y(單位:千個) | 2.156 | 3.727 | 8.305 | 24.279 | 36.224 |
注:參考數據![]() (其中z=lny).
(其中z=lny).
附:樣本(xi,yi)(i=1,2,…,n)的最小二乘法估計公式為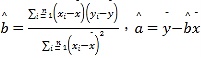
(1)根據表中數據判斷,y=a+bx與y=cedx(其中e=2.71828…,為自然對數的底數),哪一個回歸方程類型適宜預測未來幾年我國區塊鏈企業總數量?(給出結果即可,不必說明理由)
(2)根據(1)的結果,求y關于x的回歸方程(結果精確到小數點后第三位);
(3)為了促進公司間的合作與發展,區塊鏈聯合總部決定進行一次信息化技術比賽,邀請甲、乙、丙三家區塊鏈公司參賽比賽規則如下:①每場比賽有兩個公司參加,并決出勝負;②每場比賽獲勝的公司與未參加此場比賽的公司進行下一場的比賽;③在比賽中,若有一個公司首先獲勝兩場,則本次比賽結束,該公司就獲得此次信息化比賽的“優勝公司”,已知在每場比賽中,甲勝乙的概率為![]() ,甲勝丙的概率為
,甲勝丙的概率為![]() ,乙勝丙的概率為
,乙勝丙的概率為![]() ,請通過計算說明,哪兩個公司進行首場比賽時,甲公司獲得“優勝公司”的概率最大?
,請通過計算說明,哪兩個公司進行首場比賽時,甲公司獲得“優勝公司”的概率最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P-ABCD的底面是正方形,![]() 底面ABCD,
底面ABCD,![]() ,E是側棱的中點.
,E是側棱的中點.
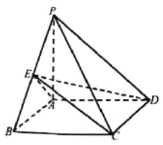
(1)求異面直線AE與PD所成的角;
(2)求點B到平面ECD的距離
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側面
中,側面![]() 為等邊三角形,且垂直于底面
為等邊三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的中點.
的中點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)已知點![]() 在棱
在棱![]() 上且
上且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,側面PAD是等邊三角形,且平面
中,側面PAD是等邊三角形,且平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() .
.
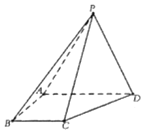
(1)AD上是否存在一點M,使得平面![]() 平面ABCD;若存在,請證明,若不存在,請說明理由;
平面ABCD;若存在,請證明,若不存在,請說明理由;
(2)若![]() 的面積為
的面積為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
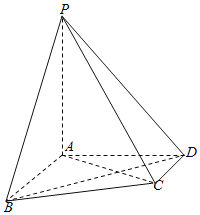
(1)證明:![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)設Q為線段PD上的點,且直線AQ和平面PAC所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com