
【題目】設a∈R,數列{an}滿足a1=a,an+1=an﹣(an﹣2)3,則( )
A.當a=4時,a10>210B.當![]() 時,a10>2
時,a10>2
C.當![]() 時,a10>210D.當
時,a10>210D.當![]() 時,a10>2
時,a10>2
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心為原點
的中心為原點![]() ,左焦點為
,左焦點為![]() ,離心率為
,離心率為![]() ,不與坐標軸垂直的直線
,不與坐標軸垂直的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點.
兩點.
(1)若![]() 為線段
為線段![]() 的中點,求直線
的中點,求直線![]() 的方程.
的方程.
(2)若點![]() 是直線
是直線![]() 上一點,點
上一點,點![]() 在橢圓
在橢圓![]() 上,且滿足
上,且滿足![]() ,設直線
,設直線![]() 與直線
與直線![]() 的斜率分別為
的斜率分別為![]() ,問:
,問: ![]() 是否為定值?若是.請求出
是否為定值?若是.請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某民族品牌手機生產商為迎合市場需求,每年都會研發推出一款新型號手機.該公司現研發了一款新型智能手機并投入生產,生產這款手機的月固定成本為80萬元,每生產1千臺,須另投入27萬元, 設該公司每月生產![]() 千臺并能全部銷售完,每1千臺的銷售收入為
千臺并能全部銷售完,每1千臺的銷售收入為![]() 萬元,且
萬元,且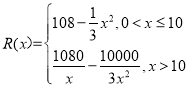 .為更好推廣該產品,手機生產商每月還支付各類廣告費用20萬元.
.為更好推廣該產品,手機生產商每月還支付各類廣告費用20萬元.
(Ⅰ)寫出月利潤![]() (萬元)關于月產量
(萬元)關于月產量![]() (千臺)的函數解析式;
(千臺)的函數解析式;
(Ⅱ)當月產量為多少千臺時,該公司在這一型號的手機生產中所獲月利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】流行性感冒(簡稱流感)是流感病毒引起的急性呼吸道感染,是一種傳染性強、傳播速度快的疾病.其主要通過空氣中的飛沫、人與人之間的接觸或與被污染物品的接觸傳播.流感每年在世界各地均有傳播,在我國北方通常呈冬春季流行,南方有冬春季和夏季兩個流行高峰.兒童相對免疫力低,在幼兒園、學校等人員密集的地方更容易被傳染.某幼兒園將去年春期該園患流感小朋友按照年齡與人數統計,得到如下數據:
年齡( |
|
|
|
|
|
患病人數( |
|
|
|
|
|
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)計算變量![]() 、
、![]() 的相關系數
的相關系數![]() (計算結果精確到
(計算結果精確到![]() ),并回答是否可以認為該幼兒園去年春期患流感人數與年齡負相關很強?(若
),并回答是否可以認為該幼兒園去年春期患流感人數與年齡負相關很強?(若![]() ,則
,則![]() 、
、![]() 相關性很強;若
相關性很強;若![]() ,則
,則![]() 、
、![]() 相關性一般;若
相關性一般;若![]() ,則
,則![]() 、
、![]() 相關性較弱.)
相關性較弱.)
參考數據:![]() .
.
參考公式: ,
,
相關系數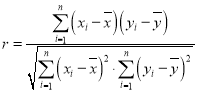 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 內,動點
內,動點![]() 到定點
到定點![]() 的距離與
的距離與![]() 到定直線
到定直線![]() 距離之比為
距離之比為![]() .
.
(Ⅰ)求動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設點![]() 是軌跡
是軌跡![]() 上兩個動點直線
上兩個動點直線![]() 與軌跡
與軌跡![]() 的另一交點分別為
的另一交點分別為![]() 且直線
且直線![]() 的斜率之積等于
的斜率之積等于![]() ,問四邊形
,問四邊形![]() 的面積
的面積![]() 是否為定值?請說明理由.
是否為定值?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二.問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中被5除余3且被7除余2的數按照從小到大的順序排成一列,構成一個數列,則該數列各項之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數學 來源: 題型:
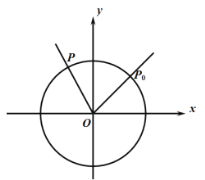
【題目】如圖,單位圓上有一點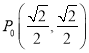 ,點
,點![]() 以點
以點![]() 為起點按逆時針方向以每秒
為起點按逆時針方向以每秒![]() 弧度作圓周運動,點
弧度作圓周運動,點![]() 的縱坐標
的縱坐標![]() 是關于時間
是關于時間![]() 的函數,記作
的函數,記作![]() .
.
(1)當![]() 時,求
時,求![]() ;
;
(2)若將函數![]() 向左平移
向左平移![]() 個單位長度后,得到的曲線關于
個單位長度后,得到的曲線關于![]() 軸對稱,求
軸對稱,求![]() 的最小正值,并求此時
的最小正值,并求此時![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為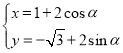 (其中
(其中![]() 為參數,
為參數,![]() ).在極坐標系(以坐標原點
).在極坐標系(以坐標原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,曲線
軸非負半軸為極軸)中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 上恰有一個點到曲線
上恰有一個點到曲線![]() 的距離為1,求曲線
的距離為1,求曲線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的圖象的兩條相鄰對稱軸之間的距離為
)的圖象的兩條相鄰對稱軸之間的距離為![]() ,且圖象上一個最低點為
,且圖象上一個最低點為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)當![]() 時,求函數
時,求函數![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有兩個不相等的實數根
上有兩個不相等的實數根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com