
【題目】過橢圓W:![]() 的左焦點(diǎn)
的左焦點(diǎn)![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn),其中
兩點(diǎn),其中![]()
![]() ,另一條過
,另一條過![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點(diǎn)(不與
兩點(diǎn)(不與![]() 重合),且
重合),且![]() 點(diǎn)不與點(diǎn)
點(diǎn)不與點(diǎn)![]() 重合.過
重合.過![]() 作
作![]() 軸的垂線分別交直線
軸的垂線分別交直線![]() ,
,![]() 于
于![]() ,
,![]() .
.
(Ⅰ)求![]() 點(diǎn)坐標(biāo)和直線
點(diǎn)坐標(biāo)和直線![]() 的方程;
的方程;
(Ⅱ)求證:![]() .
.
【答案】(Ⅰ)![]() ,
,![]() 的方程為
的方程為![]() ;(Ⅱ)詳見解析.
;(Ⅱ)詳見解析.
【解析】
(Ⅰ)由題意可得直線![]() 的方程為
的方程為![]() .與橢圓方程聯(lián)立方程組,即可求解B點(diǎn)坐標(biāo);
.與橢圓方程聯(lián)立方程組,即可求解B點(diǎn)坐標(biāo);
(Ⅱ)設(shè)![]() ,
,![]() ,
,![]() 的方程為
的方程為![]() ,聯(lián)立方程組,根據(jù)根與系數(shù)的關(guān)系,求得
,聯(lián)立方程組,根據(jù)根與系數(shù)的關(guān)系,求得![]() ,
,![]() ,進(jìn)而得出
,進(jìn)而得出![]() 點(diǎn)的縱坐標(biāo)
點(diǎn)的縱坐標(biāo)![]() ,化簡即可證得
,化簡即可證得![]() ,得到證明.
,得到證明.
(Ⅰ)由題意可得直線![]() 的方程為
的方程為![]() .與橢圓方程聯(lián)立,由
.與橢圓方程聯(lián)立,由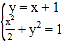
可求![]() .
.
(Ⅱ)當(dāng)![]() 與
與![]() 軸垂直時(shí),
軸垂直時(shí),![]() 兩點(diǎn)與
兩點(diǎn)與![]() ,
,![]() 兩點(diǎn)重合,由橢圓的對(duì)稱性,
兩點(diǎn)重合,由橢圓的對(duì)稱性,![]() .
.
當(dāng)![]() 不與
不與![]() 軸垂直時(shí),
軸垂直時(shí),
設(shè)![]() ,
,![]() ,
,![]() 的方程為
的方程為![]() (
(![]() ).
).
由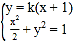 消去
消去![]() ,整理得
,整理得![]() .
.
則![]() ,
,![]() .
.
由已知,![]() ,
,
則直線![]() 的方程為
的方程為![]() ,令
,令![]() ,得點(diǎn)
,得點(diǎn)![]() 的縱坐標(biāo)
的縱坐標(biāo)![]() .把
.把![]() 代入得
代入得![]() .
.
由已知,![]() ,則直線
,則直線![]() 的方程為
的方程為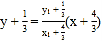 ,令
,令![]() ,得點(diǎn)
,得點(diǎn)![]() 的縱坐標(biāo)
的縱坐標(biāo)![]() .把
.把![]() 代入得
代入得![]() .
.
![]()
![]()
![]()
把![]() ,
,![]() 代入到
代入到![]() 中,
中,
![]() =
=![]() .
.
即![]() ,即
,即![]() ..
..


 長江作業(yè)本同步練習(xí)冊(cè)系列答案
長江作業(yè)本同步練習(xí)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ,給出下列命題:
,給出下列命題:
①若![]() ,則
,則![]() ; ②若
; ②若![]() ,則
,則![]() ;
;
③若![]() ,則
,則![]() ; ④若
; ④若![]() ,則
,則![]() .
.
其中正確命題的序號(hào)是_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() ,點(diǎn)
,點(diǎn)![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的離心率是
的離心率是![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)點(diǎn)![]() 為橢圓長軸的左端點(diǎn),
為橢圓長軸的左端點(diǎn),![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點(diǎn)的兩點(diǎn),記直線
長軸端點(diǎn)的兩點(diǎn),記直線![]() 斜率分別為
斜率分別為![]() ,若
,若![]() ,請(qǐng)判斷直線
,請(qǐng)判斷直線![]() 是否過定點(diǎn)?若過定點(diǎn),求該定點(diǎn)坐標(biāo),若不過定點(diǎn),請(qǐng)說明理由.
是否過定點(diǎn)?若過定點(diǎn),求該定點(diǎn)坐標(biāo),若不過定點(diǎn),請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年國際象棋奧林匹克團(tuán)體賽中國男隊(duì)、女隊(duì)同時(shí)奪冠.國際象棋中騎士的移動(dòng)規(guī)則是沿著3×2格或2×3格的對(duì)角移動(dòng).在歷史上,歐拉、泰勒、哈密爾頓等數(shù)學(xué)家研究了“騎士巡游”問題:在![]() 格的黑白相間的國際象棋棋盤上移動(dòng)騎士,是否可以讓騎士從某方格內(nèi)出發(fā)不重復(fù)地走遍棋盤上的每一格?
格的黑白相間的國際象棋棋盤上移動(dòng)騎士,是否可以讓騎士從某方格內(nèi)出發(fā)不重復(fù)地走遍棋盤上的每一格?
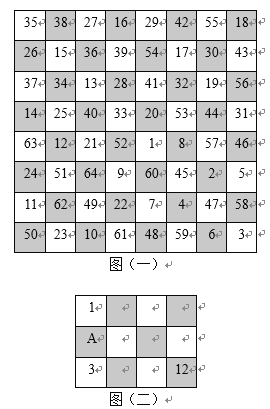
圖(一)給出了騎士的一種走法,它從圖上標(biāo)1的方格內(nèi)出發(fā),依次經(jīng)過標(biāo)2,3,4,5,6,![]() ,到達(dá)標(biāo)64的方格內(nèi),不重復(fù)地走遍棋盤上的每一格,又可從標(biāo)64的方格內(nèi)直接走回到標(biāo)1的方格內(nèi).如果騎士的出發(fā)點(diǎn)在左下角標(biāo)50的方格內(nèi),按照上述走法,_____(填“能”或“不能”)走回到標(biāo)50的方格內(nèi).
,到達(dá)標(biāo)64的方格內(nèi),不重復(fù)地走遍棋盤上的每一格,又可從標(biāo)64的方格內(nèi)直接走回到標(biāo)1的方格內(nèi).如果騎士的出發(fā)點(diǎn)在左下角標(biāo)50的方格內(nèi),按照上述走法,_____(填“能”或“不能”)走回到標(biāo)50的方格內(nèi).
若騎士限制在圖(二)中的3×4=12格內(nèi)按規(guī)則移動(dòng),存在唯一一種給方格標(biāo)數(shù)字的方式,使得騎士從左上角標(biāo)1的方格內(nèi)出發(fā),依次不重復(fù)經(jīng)過2,3,4,5,6,![]() ,到達(dá)右下角標(biāo)12的方格內(nèi),分析圖(二)中A處所標(biāo)的數(shù)應(yīng)為____.
,到達(dá)右下角標(biāo)12的方格內(nèi),分析圖(二)中A處所標(biāo)的數(shù)應(yīng)為____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,
,![]() ,記
,記![]() .
.
(1)求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)當(dāng)![]() 時(shí),若函數(shù)
時(shí),若函數(shù)![]() 沒有零點(diǎn),求
沒有零點(diǎn),求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=2x和g(x)=2x的圖象如圖所示,設(shè)兩函數(shù)的圖象交于點(diǎn)A(x1,y1),B(x2,y2),且x1<x2.

(1)請(qǐng)指出圖中曲線C1,C2分別對(duì)應(yīng)的函數(shù);
(2)結(jié)合函數(shù)圖象,判斷![]() 與
與![]() ,f(2 019)與g(2 019)的大小.
,f(2 019)與g(2 019)的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知三棱錐![]() 的所有頂點(diǎn)都在球
的所有頂點(diǎn)都在球![]() 的球面上,
的球面上,![]() 平面
平面![]() ,
,![]() ,
,![]() ,若球
,若球![]() 的表面積為
的表面積為![]() ,則三棱錐
,則三棱錐![]() 的側(cè)面積的最大值為( )
的側(cè)面積的最大值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某超市在節(jié)日期間進(jìn)行有獎(jiǎng)促銷,凡在該超市購物滿![]() 元的顧客,將獲得一次摸獎(jiǎng)機(jī)會(huì),規(guī)則如下:一個(gè)袋子裝有
元的顧客,將獲得一次摸獎(jiǎng)機(jī)會(huì),規(guī)則如下:一個(gè)袋子裝有![]() 只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎(jiǎng)勵(lì)
只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎(jiǎng)勵(lì)![]() 元;共兩只球都是綠色,則獎(jiǎng)勵(lì)
元;共兩只球都是綠色,則獎(jiǎng)勵(lì)![]() 元;若兩只球顏色不同,則不獎(jiǎng)勵(lì).
元;若兩只球顏色不同,則不獎(jiǎng)勵(lì).
(1)求一名顧客在一次摸獎(jiǎng)活動(dòng)中獲得![]() 元的概率;
元的概率;
(2)記![]() 為兩名顧客參與該摸獎(jiǎng)活動(dòng)獲得的獎(jiǎng)勵(lì)總數(shù)額,求隨機(jī)變量
為兩名顧客參與該摸獎(jiǎng)活動(dòng)獲得的獎(jiǎng)勵(lì)總數(shù)額,求隨機(jī)變量![]() 的分布列和數(shù)學(xué)期望.
的分布列和數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() .
.
(1)過原點(diǎn)![]() 的直線
的直線![]() 被圓
被圓![]() 所截得的弦長為2,求直線
所截得的弦長為2,求直線![]() 的方程;
的方程;
(2)過![]() 外的一點(diǎn)
外的一點(diǎn)![]() 向圓
向圓![]() 引切線
引切線![]() ,
,![]() 為切點(diǎn),
為切點(diǎn),![]() 為坐標(biāo)原點(diǎn),若
為坐標(biāo)原點(diǎn),若![]() ,求使
,求使![]() 最短時(shí)的點(diǎn)
最短時(shí)的點(diǎn)![]() 坐標(biāo).
坐標(biāo).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com