
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
��1����![]() ��ԇ��(sh��)
��ԇ��(sh��)![]() �����c(di��n)��(g��)��(sh��)��
�����c(di��n)��(g��)��(sh��)��
��2����(d��ng)![]() ����(du��)
����(du��)![]() ��
��![]() �ҝM��
�ҝM��![]() ��ԇ�Д�
��ԇ�Д�![]() �c
�c![]() �Ĵ�С�P(gu��n)ϵ�����f������.
�Ĵ�С�P(gu��n)ϵ�����f������.
���𰸡���1��һ��(g��)���c(di��n)����2��![]() ������Ҋ����
������Ҋ����
��������
��1����![]() ���뺯��(sh��)����ʽ�������(d��o)����(sh��)�����Ì�(d��o)��(sh��)�c����(sh��)���{(di��o)��֮�g���P(gu��n)ϵ�������(sh��)�����ֵ���M(j��n)���ɴ_������(sh��)�����c(di��n)��
���뺯��(sh��)����ʽ�������(d��o)����(sh��)�����Ì�(d��o)��(sh��)�c����(sh��)���{(di��o)��֮�g���P(gu��n)ϵ�������(sh��)�����ֵ���M(j��n)���ɴ_������(sh��)�����c(di��n)��
��2����![]() ���뺯��(sh��)�Ľ���ʽ����
���뺯��(sh��)�Ľ���ʽ����![]() ����
����![]() ����
����![]() ���ɵ�
���ɵ�![]() �����Ì�(d��o)��(sh��)�ɵ�
�����Ì�(d��o)��(sh��)�ɵ�![]() ���Ķ��ɵ�
���Ķ��ɵ�![]() ���M(j��n)���ɱ��^����С��
���M(j��n)���ɱ��^����С��
��1����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ��
��
�˕r(sh��)![]() ��
��
�t��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����(d��ng)
����(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��
��֪����(sh��)![]() �څ^(q��)�g
�څ^(q��)�g![]() ���{(di��o)�f�����څ^(q��)�g
���{(di��o)�f�����څ^(q��)�g![]() ���{(di��o)�f�p��
���{(di��o)�f�p��
����![]() ����(d��ng)�҃H��(d��ng)
����(d��ng)�҃H��(d��ng)![]() ȡ��̖(h��o)����
ȡ��̖(h��o)����
�ʮ�(d��ng)![]() �r(sh��)������(sh��)
�r(sh��)������(sh��)![]() ֻ��һ��(g��)���c(di��n)��
ֻ��һ��(g��)���c(di��n)��
��2��![]() ���������£���(d��ng)
���������£���(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() ��
��
��![]() ����
����![]() ��
��
�Ķ�![]() ����
����![]() ��
��
�t��![]() ����
����![]() ��
��
��֪��![]() �څ^(q��)�g
�څ^(q��)�g![]() �φ��{(di��o)�f�p���څ^(q��)�g
�φ��{(di��o)�f�p���څ^(q��)�g![]() �φ��{(di��o)�f��.
�φ��{(di��o)�f��.
������![]() ������
������![]() ��
��
��ˣ�![]() �����Ͽ�֪���@��ȡ����̖(h��o)��Ҫ
�����Ͽ�֪���@��ȡ����̖(h��o)��Ҫ![]() ��
��
���˕r(sh��)![]() �o��(sh��)��(sh��)�⣬�ʱ���
�o��(sh��)��(sh��)�⣬�ʱ���![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)
ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)![]() ���t����
���t����![]() ���н�ĺ͞飨 ��
���н�ĺ͞飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������(sh��)�W(xu��)�ҵ�������(Dirichlet,1805~1859)�ڔ�(sh��)�W(xu��)�I(l��ng)��ɾ��@��.19���o(j��),���������x��һ��(g��)����ֵĺ���(sh��)�� 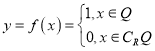 ����R�錍(sh��)��(sh��)��,Q�����픵(sh��)��.�t�P(gu��n)�ں���(sh��)
����R�錍(sh��)��(sh��)��,Q�����픵(sh��)��.�t�P(gu��n)�ں���(sh��)![]() �������Ă�(g��)���},���_�Ğ�( )
�������Ă�(g��)���},���_�Ğ�( )
A.����(sh��)![]() ��ż����(sh��)
��ż����(sh��)
B.![]() ,
,![]() ,
,![]() �����
�����
C.��ȡһ��(g��)����������픵(sh��)T,![]() ��(du��)�����
��(du��)�����![]() �����
�����
D.����������(g��)�c(di��n)![]() ,
,![]() ,
,![]() ,ʹ��
,ʹ��![]() �����ֱ��������
�����ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ˆT���M(j��n)����վ���ij�(xi��ng)���и�ݗ��Σ�U(xi��n)���΄�(w��)��ÿ��ֻ��һ��(g��)���M(j��n)ȥ����ÿ��(g��)��ֻ��һ�Σ������r(sh��)�g�����^10��犣����ǰһ��(g��)��10��犃�(n��i)��������΄�(w��)�t������������һ��(g��)��.�F(xi��n)��һ��ֻ�мס��ҡ�������(g��)�˿��ɣ���������������΄�(w��)�ĸ��ʷքe��![]() ��
��![]() ��
��![]() �����O(sh��)
�����O(sh��)![]() ��
��![]() ��
��![]() ������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼����(d��)��.
������ȣ��Ҽٶ������ܷ�����΄�(w��)���¼����(d��)��.
��1������������ȣ��Ҵ�֮��������������ˣ����΄�(w��)�ܱ���ɵĸ���.����׃?n��i)���(g��)�˱��ɳ����Ⱥ�����΄�(w��)�ܱ���ɵĸ����Ƿ�l(f��)��׃����
��2���ٶ�![]() ��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�Ĕ�(sh��)�W(xu��)�����_(d��)����С.
��ԇ���������ӵ��Ⱥ�����ɳ��ˆT����ʹ�����ɳ����ˆT��(sh��)Ŀ�Ĕ�(sh��)�W(xu��)�����_(d��)����С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ������e����Ȼ��(du��)��(sh��)�ĵף�.
������e����Ȼ��(du��)��(sh��)�ĵף�.
��1����![]() ��
��![]() �φ��{(di��o)�f������(sh��)��(sh��)a��ȡֵ������
�φ��{(di��o)�f������(sh��)��(sh��)a��ȡֵ������
��2����![]() ���C����
���C����![]() ����Ψһ�ĘOСֵ�c(di��n)
����Ψһ�ĘOСֵ�c(di��n)![]() ����
����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ��
��
����ӛ![]() ��ԇ�Дຯ��(sh��)
��ԇ�Дຯ��(sh��)![]() �ĘOֵ�c(di��n)����r��
�ĘOֵ�c(di��n)����r��
������![]() ���҃H�Ѓɂ�(g��)����(sh��)�⣬��(sh��)��(sh��)
���҃H�Ѓɂ�(g��)����(sh��)�⣬��(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ![]() �У�ֱ��
�У�ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�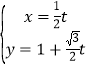 ��
��![]() �酢��(sh��)������������(bi��o)ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)������������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�������S��O�S�ĘO����(bi��o)ϵ�У�����
�S�������S��O�S�ĘO����(bi��o)ϵ�У�����![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��
��![]() ��
��![]() ��.
��.
��I����ֱ��![]() �ĘO����(bi��o)���̼�����
�ĘO����(bi��o)���̼�����![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
������֪![]() ��ֱ��
��ֱ��![]() �ϵ�һ�c(di��n)��
�ϵ�һ�c(di��n)��![]() ������
������![]() �ϵ�һ�c(di��n)��
�ϵ�һ�c(di��n)�� ![]() ��
��![]() ����
����![]() �����ֵ��2����
�����ֵ��2����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
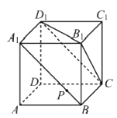
���}Ŀ����D���������w![]() �У��c(di��n)
�У��c(di��n)![]() �ھ���
�ھ���![]() ���Ƅ�(d��ng)���������Дࣺ��ƽ��
���Ƅ�(d��ng)���������Дࣺ��ƽ��![]() ƽ��
ƽ��![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ���������F
���������F![]() ���w�e��׃����
���w�e��׃����![]() ƽ��
ƽ��![]() �����У����_����______�������������_���Д����̖(h��o)�����ϣ�
�����У����_����______�������������_���Д����̖(h��o)�����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�з��ܾ֞����˽�ԓ������![]() ��
��![]() ����
����![]() ��
��![]() �����g�I���ַ���r�������S�C(j��)�������
�����g�I���ַ���r�������S�C(j��)�������![]() ��ُ���ߣ�����(du��)��ُ����e
��ُ���ߣ�����(du��)��ُ����e![]() ����λ��ƽ���ף�
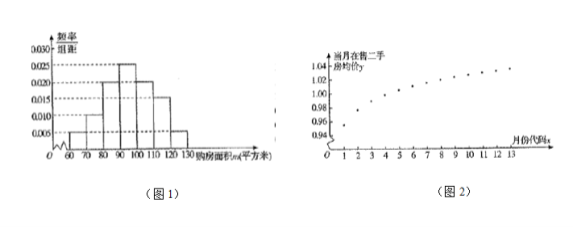
����λ��ƽ���ף�![]() ���M(j��n)����һ���{(di��o)��y(t��ng)Ӌ(j��)���Ƴ�����D
���M(j��n)����һ���{(di��o)��y(t��ng)Ӌ(j��)���Ƴ�����D![]() ��ʾ���l�ʷֲ�ֱ���D�������{(di��o)����ԓ��
��ʾ���l�ʷֲ�ֱ���D�������{(di��o)����ԓ��![]() ��
��![]() ����
����![]() ��
��![]() �����g��(d��ng)�����۶��ַ����r(ji��)
�����g��(d��ng)�����۶��ַ����r(ji��)![]() ����λ���fԪ/ƽ���ף����Ƴ�����D
����λ���fԪ/ƽ���ף����Ƴ�����D![]() ��ʾ��ɢ�c(di��n)�D���D���·ݴ��a
��ʾ��ɢ�c(di��n)�D���D���·ݴ��a![]() �քe��(du��)��(y��ng)
�քe��(du��)��(y��ng)![]() ��
��![]() ����
����![]() ��
��![]() �£�.
�£�.
��1��ԇ��Ӌ(j��)ԓ�������ُ����e����λ��(sh��)![]() ��
��
��2���F(xi��n)���÷ӳ�ӵķ�����ُ����eλ��![]() ��
��![]() λ�������S�C(j��)��ȡ
λ�������S�C(j��)��ȡ![]() �ˣ��ُ��@
�ˣ��ُ��@![]() �����S�C(j��)��ȡ
�����S�C(j��)��ȡ![]() �ˣ����@
�ˣ����@![]() �˵�ُ����eǡ����һ����
�˵�ُ����eǡ����һ����![]() �ĸ��ʣ�
�ĸ��ʣ�
��3������(j��)ɢ�c(di��n)�D�x��![]() ��
��![]() �ɂ�(g��)ģ���M(j��n)�ДM�ϣ���(j��ng)�^��(sh��)��(j��)̎���õ��ɂ�(g��)�ؚw���̣��քe��
�ɂ�(g��)ģ���M(j��n)�ДM�ϣ���(j��ng)�^��(sh��)��(j��)̎���õ��ɂ�(g��)�ؚw���̣��քe��![]() ��
��![]() �����õ�һЩ�y(t��ng)Ӌ(j��)����ֵ���±���ʾ��
�����õ�һЩ�y(t��ng)Ӌ(j��)����ֵ���±���ʾ��
|
| |
| 0.000591 | 0.000164 |
| 0.006050 | |
Ո(q��ng)�������P(gu��n)ָ��(sh��)![]() �Д��Ă�(g��)ģ�͵ĔM��Ч�����ã����ÔM��Ч�����õ�ģ���A(y��)�y(c��)��
�Д��Ă�(g��)ģ�͵ĔM��Ч�����ã����ÔM��Ч�����õ�ģ���A(y��)�y(c��)��![]() ��
��![]() �·ݵĶ��ַ�ُ�����r(ji��)�����_��
�·ݵĶ��ַ�ُ�����r(ji��)�����_��![]() ��
��
��������(sh��)��(j��)��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��������ʽ��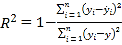
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com