
【題目】已知f(x)=2x2+bx+c.
(1)對(duì)任意x∈[﹣1,1],f(x)的最大值與最小值之差不大于6,求b的取值范圍;
(2)若f(x)=0有兩個(gè)不同實(shí)根,f(f(x))無零點(diǎn),求證: ![]() ﹣
﹣ ![]() >1.
>1.
【答案】
(1)解:f(x)=2x2+bx+c= ![]() +c﹣
+c﹣ ![]() ,x∈[﹣1,1].
,x∈[﹣1,1].
①當(dāng)﹣ ![]() ≤﹣1,即b≥4時(shí),函數(shù)f(x)在x∈[﹣1,1]單調(diào)遞增,∴f(1)﹣f(﹣1)≤6,化為:b≤3,舍去;
≤﹣1,即b≥4時(shí),函數(shù)f(x)在x∈[﹣1,1]單調(diào)遞增,∴f(1)﹣f(﹣1)≤6,化為:b≤3,舍去;
②當(dāng)﹣ ![]() ≥1,即b≤﹣4時(shí),函數(shù)f(x)在x∈[﹣1,1]單調(diào)遞減,∴f(﹣1)﹣f(1)≤6,化為:b≥﹣3,舍去;
≥1,即b≤﹣4時(shí),函數(shù)f(x)在x∈[﹣1,1]單調(diào)遞減,∴f(﹣1)﹣f(1)≤6,化為:b≥﹣3,舍去;
③當(dāng)﹣1<﹣ ![]() <1,即﹣4<b<4時(shí),函數(shù)f(x)在
<1,即﹣4<b<4時(shí),函數(shù)f(x)在 ![]() 內(nèi)單調(diào)遞減,在
內(nèi)單調(diào)遞減,在 ![]() 內(nèi)單調(diào)遞增,∴f(x)min=c﹣
內(nèi)單調(diào)遞增,∴f(x)min=c﹣ ![]() .
.
∵f(1)﹣f(﹣1)=2b,當(dāng)0≤b<4時(shí),f(x)max=f(1)=2+b+c,則2+b+c﹣ ![]() ≤6,解得0≤b≤
≤6,解得0≤b≤ ![]() .
.
當(dāng)﹣4<b<0時(shí),f(x)max=f(﹣1)=2﹣b+c,則2﹣b+c﹣ ![]() ≤6,解得
≤6,解得 ![]() ≤b<0.
≤b<0.
綜上可得:b的取值范圍是 ![]()
(2)證明:f(x)=2x2+bx+c=0有兩個(gè)不同實(shí)根,∴△=b2﹣8c>0.
可得此方程的兩個(gè)實(shí)數(shù)根:x1= ![]() ,x2=
,x2= ![]() .
.
要使f(f(x))無零點(diǎn),則方程f(x)=x1,f(x)=x2,均無解.
∵x1>x2,∴f(x)=2x2+bx+c的最小值c﹣ ![]() >x1=
>x1= ![]() ,即b2﹣8c+2
,即b2﹣8c+2 ![]() +1<2b+1,
+1<2b+1,
∴ ![]() <2b+1,∴
<2b+1,∴ ![]() +1<
+1< ![]() .
.
∴ ![]() ﹣
﹣ ![]() >1
>1
【解析】(1)f(x)=2x2+bx+c= ![]() +c﹣
+c﹣ ![]() ,x∈[﹣1,1].對(duì)b分類討論,利用二次函數(shù)的單調(diào)性即可得出.(2)f(x)=2x2+bx+c=0有兩個(gè)不同實(shí)根,可得△>0.可得此方程的兩個(gè)實(shí)數(shù)根:x1=
,x∈[﹣1,1].對(duì)b分類討論,利用二次函數(shù)的單調(diào)性即可得出.(2)f(x)=2x2+bx+c=0有兩個(gè)不同實(shí)根,可得△>0.可得此方程的兩個(gè)實(shí)數(shù)根:x1= ![]() ,x2=
,x2= ![]() .要使f(f(x))無零點(diǎn),則方程f(x)=x1 , f(x)=x2 , 均無解.由于x1>x2 , 可得f(x)=2x2+bx+c的最小值c﹣
.要使f(f(x))無零點(diǎn),則方程f(x)=x1 , f(x)=x2 , 均無解.由于x1>x2 , 可得f(x)=2x2+bx+c的最小值c﹣ ![]() >x1 , 化簡(jiǎn)整理即可證明.
>x1 , 化簡(jiǎn)整理即可證明.


 同步練習(xí)強(qiáng)化拓展系列答案
同步練習(xí)強(qiáng)化拓展系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了了解初三女生身高情況,某中學(xué)對(duì)初三女生身高情況進(jìn)行了一次測(cè)量,所得數(shù)據(jù)整理后列出了頻率分布表如下:
組 別 | 頻數(shù) | 頻率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 計(jì) | M | N |
(1)求出表中m,n,M,N所表示的數(shù)分別是多少?
(2)畫出頻率分布直方圖;
(3)全體女生中身高在哪組范圍內(nèi)的人數(shù)最多?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的三個(gè)頂點(diǎn)A(m,n)、B(2,1)、C(﹣2,3);
(1)求BC邊所在直線的方程;
(2)BC邊上中線AD的方程為2x﹣3y+6=0,且S△ABC=7,求點(diǎn)A的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
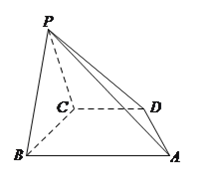
【題目】在四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 和平面
和平面![]() 所成二面角(小于
所成二面角(小于![]() )的大小.
)的大小.
(Ⅲ)在棱![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() 使得
使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請(qǐng)說明理由.
的值;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】張老師開車上班,有路線①與路線②兩條路線可供選擇. 路線①:沿途有![]() 兩處獨(dú)立運(yùn)行的交通信號(hào)燈,且兩處遇到綠燈的概率依次為
兩處獨(dú)立運(yùn)行的交通信號(hào)燈,且兩處遇到綠燈的概率依次為![]() ,若
,若![]() 處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間2分鐘;若
處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間2分鐘;若![]() 處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間3分鐘;若兩處都遇綠燈,則全程所花時(shí)間為20分鐘.
處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間3分鐘;若兩處都遇綠燈,則全程所花時(shí)間為20分鐘.
路線②:沿途有![]() 兩處獨(dú)立運(yùn)行的交通信號(hào)燈,且兩處遇到綠燈的概率依次為
兩處獨(dú)立運(yùn)行的交通信號(hào)燈,且兩處遇到綠燈的概率依次為![]() ,若
,若![]() 處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間8分鐘;若
處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間8分鐘;若![]() 處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間5分鐘;若兩處都遇綠燈,則全程所花時(shí)間為15分鐘.
處遇紅燈或黃燈,則導(dǎo)致延誤時(shí)間5分鐘;若兩處都遇綠燈,則全程所花時(shí)間為15分鐘.
(1)若張老師選擇路線①,求他20分鐘能到校的概率;
(2)為使張老師日常上班途中所花時(shí)間較少,你建議張老師選擇哪條路線?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在等差數(shù)列{an}中,a2=11,a5=5.
(1)求通項(xiàng)公式an;
(2)求前n項(xiàng)和Sn的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義域?yàn)镽的函數(shù)f(x)= ![]() 是奇函數(shù).
是奇函數(shù).
(1)求a,b的值;
(2)解不等式f(x)< ![]() ;
;
(3)求f(x)的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=(1﹣x)|x﹣3|在(﹣∞,a]上取得最小值﹣1,則實(shí)數(shù)a的取值范圍是( )
A.(﹣∞,2]
B.![]()
C.![]()
D.[2,+∞)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() 是自然對(duì)數(shù)的底數(shù)),
是自然對(duì)數(shù)的底數(shù)),![]()
(1)求曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)設(shè)![]() ,其中
,其中![]() 為
為![]() 的導(dǎo)函數(shù),證明:對(duì)任意
的導(dǎo)函數(shù),證明:對(duì)任意![]() ,
, ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com