
【題目】已知中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 的離心率為
的離心率為![]() ,且經過點
,且經過點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在過點![]() 的直線
的直線![]() 與
與![]() 相交于不同的兩點
相交于不同的兩點![]() ,滿足
,滿足![]() ?
?
若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的公差d>0,則下列四個命題:
的公差d>0,則下列四個命題:
①數列![]() 是遞增數列; ②數列
是遞增數列; ②數列![]() 是遞增數列;
是遞增數列;
③數列![]() 是遞增數列; ④數列
是遞增數列; ④數列![]() 是遞增數列.
是遞增數列.
其中正確命題的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為
中,△ABC是等邊三角形,AB⊥AD,CB⊥CD,點P是AC的中點,記△BPD、△ABD的面積分別為![]() ,
,![]() ,二面角A-BD-C的大小為
,二面角A-BD-C的大小為![]() ,
,
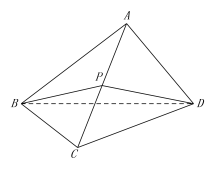
證明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校研究性學習小組對該校高三學生視力情況進行調查,在高三全體![]() 名學生中隨機抽取了
名學生中隨機抽取了![]() 名學生的體檢表,并得到如圖所示的頻率分布直方圖.
名學生的體檢表,并得到如圖所示的頻率分布直方圖.
(Ⅰ)若直方圖中后四組的頻數成等差數列,計算高三全體學生視力在![]() 以下的人數,并估計這
以下的人數,并估計這![]() 名學生視力的中位數(精確到
名學生視力的中位數(精確到![]() );
);
(Ⅱ)學習小組發現,學習成績突出的學生,近視的比較多,為了研究學生的視力與學習成績是否有關系,對高三全體成績名次在前![]() 名和后
名和后![]() 名的學生進行了調查,部分數據如表1,根據表1及臨界表2中的數據,能否在犯錯誤的概率不超過
名的學生進行了調查,部分數據如表1,根據表1及臨界表2中的數據,能否在犯錯誤的概率不超過![]() 的前提下認為視力與學習成績有關系?
的前提下認為視力與學習成績有關系?

年段名次 是否近視 | 前 | 后 |
近 視 |
| |
|
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
(參考公式:  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的方程是:
的方程是: ![]() ,以坐標原點為極點,
,以坐標原點為極點, ![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)設過原點的直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年元旦期間,某運動服裝專賣店舉辦了一次有獎促銷活動,消費每超過400元均可參加1次抽獎活動,抽獎方案有兩種,顧客只能選擇其中的一種.
方案一:顧客轉動十二等分且質地均勻的圓形轉盤(如圖),轉盤停止轉動時指針指向哪個扇形區域,則顧客可直接獲得該區域對應面額(單位:元)的現金優惠,且允許顧客轉動3次.
方案二:顧客轉動十二等分且質地均勻的圓形轉盤(如圖〕,轉盤停止轉動時指針若指向陰影部分,則未中獎,若指向白色區域,則顧客可直接獲得40元現金,且允許顧客轉動3次.

(1)若兩位顧客均獲得1次抽獎機會,且都選擇抽獎方案一,試求這兩位顧客均獲得180元現金優惠的概率;
(2)若某顧客恰好獲得1次抽獎機會.
①試分別計算他選擇兩種抽獎方案最終獲得現金獎勵的數學期望;
②從概率的角度比較①中該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,
上的點,![]() ,且
,且![]() (如圖①).將四邊形
(如圖①).將四邊形![]() 沿
沿![]() 折起,連接
折起,連接![]() 、
、![]() 、
、![]() (如圖②).在折起的過程中,則下列表述:
(如圖②).在折起的過程中,則下列表述:

①![]() 平面
平面![]() ;
;
②四點![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,則平面
,則平面![]() 平面
平面![]() ;
;
④平面![]() 與平面
與平面![]() 可能垂直.其中正確的是__________.
可能垂直.其中正確的是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() .
.
(1)求以右焦點為圓心,與雙曲線![]() 的漸近線相切的圓的方程;
的漸近線相切的圓的方程;
(2)若經過點![]() 的直線與雙曲線
的直線與雙曲線![]() 的右支交于不同兩點
的右支交于不同兩點![]() 、
、![]() ,求線段
,求線段![]() 的中垂線
的中垂線![]() 在
在![]() 軸上截距
軸上截距![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com