
【題目】已知![]() 是定義在R上的奇函數,當
是定義在R上的奇函數,當![]() 時,
時,![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)解關于![]() 的不等式
的不等式![]() ,結果用集合或區間表示.
,結果用集合或區間表示.
【答案】(1)0
(2)![]()
(3)當a>1時,不等式的解集為(1-loga2,1+loga5);當0<a<1時,不等式的解集為R.
【解析】
試題分析:解 (1)∵f(x)是奇函數,∴f(-2)=-f(2),即f(2)+f(-2)=0.
(2)當x<0時,-x>0,∴f(-x)=a-x-1.
∵f(x)是奇函數,有f(-x)=-f(x),∴f(x)=-a-x+1(x<0).
∴所求的解析式為![]() .
.
(3)不等式等價于![]() 或
或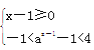 ,
,
即![]() 或
或![]() .
.
當a>1時,有![]() 或
或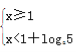 ,注意此時loga2>0,loga5>0,
,注意此時loga2>0,loga5>0,
可得此時不等式的解集為(1-loga2,1+loga5).
同理可得,當0<a<1時,不等式的解集為R.
綜上所述,當a>1時,不等式的解集為(1-loga2,1+loga5);當0<a<1時,不等式的解集為R.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓 ![]() +y2=1,A,B,C,D為橢圓上四個動點,且AC,BD相交于原點O,設A(x1 , y1),B(x2 , y2)滿足
+y2=1,A,B,C,D為橢圓上四個動點,且AC,BD相交于原點O,設A(x1 , y1),B(x2 , y2)滿足 ![]() =
= ![]() .
.
(1)求證: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否為定值,若是,請求出此定值,并求出四邊形ABCD面積的最大值,否則,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 給出下列四個命題:
給出下列四個命題:
①c = 0時,![]() 是奇函數; ②
是奇函數; ②![]() 時,方程
時,方程![]() 只有一個實根;
只有一個實根;
③![]() 的圖象關于點(0 , c)對稱; ④方程
的圖象關于點(0 , c)對稱; ④方程![]() 至多3個實根.
至多3個實根.
其中正確的命題個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
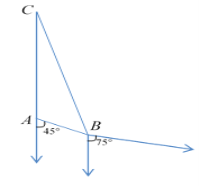
【題目】如圖,在海岸A處,發現南偏東45°方向距A為(2![]() -2)海里的B處有一艘走私船,在A處正北方向,距A為
-2)海里的B處有一艘走私船,在A處正北方向,距A為![]() 海里的C處的緝私船立即奉命以10
海里的C處的緝私船立即奉命以10![]() 海里/時的速度追截走私船.
海里/時的速度追截走私船.
(1)剛發現走私船時,求兩船的距離;
(2)若走私船正以10![]() 海里/時的速度從B處向南偏東75°方向逃竄,問緝私船沿什么方向能最快追上走私船?并求出所需要的時間(精確到分鐘,參考數據:
海里/時的速度從B處向南偏東75°方向逃竄,問緝私船沿什么方向能最快追上走私船?并求出所需要的時間(精確到分鐘,參考數據:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ex(ax2﹣x﹣1)(a∈R).
(1)若函數f(x)在R上單調遞減,求a的取值范圍
(2)當a>0時,求f(|sinx|)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點.
的中點.

(1)求四棱錐![]() 的體積;
的體積;
(2)求證: ![]() ;
;
(3)判斷線段![]() 上是否存在一點
上是否存在一點![]() (與點
(與點![]() 不重合),使得
不重合),使得![]() 四點共面? (結論不要求證明)
四點共面? (結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在![]() 中,角A,B,C的對邊分別為a,b,c,R表示
中,角A,B,C的對邊分別為a,b,c,R表示![]() 的外接圓半徑.
的外接圓半徑.
(Ⅰ)如圖,在以O圓心、半徑為2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的長;
,求弦AB的長;
(Ⅱ)在![]() 中,若
中,若![]() 是鈍角,求證:
是鈍角,求證:![]() ;
;
(Ⅲ)給定三個正實數a、b、R,其中![]() ,問:a、b、R滿足怎樣的關系時,以a、b為邊長,R為外接圓半徑的
,問:a、b、R滿足怎樣的關系時,以a、b為邊長,R為外接圓半徑的![]() 不存在、存在一個或存在兩個(全等的三角形算作同一個)?在
不存在、存在一個或存在兩個(全等的三角形算作同一個)?在![]() 存在的情況下,用a、b、R表示c.
存在的情況下,用a、b、R表示c.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若f(x)是定義在(0,+∞)上的增函數,且對一切x,y>0,滿足![]() .
.
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+3)-f(![]() )<2.
)<2.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com