
某校學習小組開展“學生語文成績與外語成績的關系”的課題研究,對該校高二年級800名學生上學期期末語文和外語成績,按優秀和不優秀分類得結果:語文和外語都優秀的有60人,語文成績優秀但外語不優秀的有140人,外語成績優秀但語文不優秀的有100人.
(Ⅰ)能否在犯錯概率不超過0.001的前提下認為該校學生的語文成績與外語成績有關系?
(Ⅱ)將上述調查所得到的頻率視為概率,從該校高二年級學生成績中,有放回地隨機抽取3名學生的成績,記抽取的3 個成績中語文,外語兩科成績至少有一科優秀的個數為X ,求X的分布列和期望E(x).
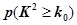 | 0.010 | 0.005 | 0.001 |
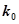 | 6.635 | 7.879 | 10.828 |
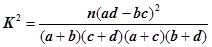
(Ⅰ)能在犯錯概率不超過0.001的前提下認為該校學生母語對于學習和掌握一門外語有關系;(Ⅱ)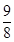 .
.
解析試題分析:(Ⅰ)根據題意得到列聯表,代入公式求解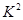 的值進行數據比較得出結論;(Ⅱ)根據題意可知X的分布滿足二項分布X~B(3,
的值進行數據比較得出結論;(Ⅱ)根據題意可知X的分布滿足二項分布X~B(3,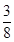 ),利用二項分布的公式直接求解.
),利用二項分布的公式直接求解.
試題解析:(Ⅰ)由題意得列聯表:
因為K2= 語文優秀 語文不優秀 總計 外語優秀 60 100 160 外語不優秀 140 500 640 總計 200 600 800  ≈16.667>10.828,
≈16.667>10.828,
所以能在犯錯概率不超過0.001的前提下認為該校學生母語對于學習和掌握一門外語有關系.5分
(Ⅱ)由已知數據,語文、外語兩科成績至少一科為優秀的頻率是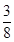 .
.
則X~B(3,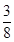 ),P(X=k)=
),P(X=k)=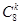 (
(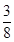 )k(
)k(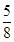 )8-k,k=0,1,2,3.
)8-k,k=0,1,2,3.
X的分布列為
E(X)=3×X 0 1 2 3 p 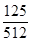

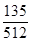
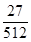
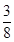 =
=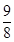 .
.
考點:1.線性相關;2.二項分布.


科目:高中數學 來源: 題型:解答題
在一次聯考后,某校對甲、乙兩個文科班的數學考試成績進行分析,規定:大于或等于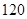 分為優秀,
分為優秀,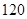 分以下為非優秀,統計成績后,得到如下的
分以下為非優秀,統計成績后,得到如下的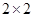 列聯表,且已知在甲、乙兩個文科班全部
列聯表,且已知在甲、乙兩個文科班全部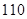 人中隨機抽取人為優秀的概率為
人中隨機抽取人為優秀的概率為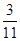 .
.
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 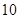 | | |
| 乙班 | | 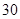 | |
| 合計 | | | 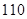 |
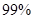 的把握認為成績與班級有關系?
的把握認為成績與班級有關系?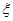 表示抽得甲班的學生人數,求
表示抽得甲班的學生人數,求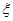 的分布列.
的分布列.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某數學老師對本校2013屆高三學生某次聯考的數學成績進行分析,按1:50進行分層抽樣抽取的20名學生的成績進行分析,分數用莖葉圖記錄如圖所示(部分數據丟失),得到頻率分布表如下:

(1)求表中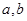 的值及分數在
的值及分數在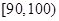 范圍內的學生數,并估計這次考試全校學生數學成績及格率(分數在
范圍內的學生數,并估計這次考試全校學生數學成績及格率(分數在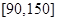 范圍為及格);
范圍為及格);
(2)從大于等于110分的學生中隨機選2名學生得分,求2名學生的平均得分大于等于130分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的50位顧客的相關數據,如下表所示:
一次購物量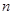 (件) (件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顧客數(人) |  | 20 | 10 | 5 | 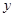 |
| 結算時間(分鐘/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
 與
與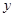 的值;
的值; 的分布列與數學期望;
的分布列與數學期望;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
將編號為1,2,3,4的四個小球,分別放入編號為1,2,3,4的四個盒子,每個盒子中有且僅有一個小球.若小球的編號與盒子的編號相同,得1分,否則得0分.記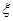 為四個小球得分總和.
為四個小球得分總和.
(1)求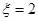 時的概率;
時的概率;
(2)求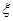 的概率分布及數學期望.
的概率分布及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)甲、乙等 名同學參加某高校的自主招生面試,已知采用抽簽的方式隨機確定各考生的面試順序(序號為
名同學參加某高校的自主招生面試,已知采用抽簽的方式隨機確定各考生的面試順序(序號為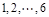 ).
).
(Ⅰ)求甲、乙兩考生的面試序號至少有一個為奇數的概率;
(Ⅱ)記在甲、乙兩考生之間參加面試的考生人數為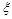 ,求隨機變量
,求隨機變量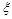 的分布列與期望.
的分布列與期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某高校在2013年的自主招生考試成績中隨機抽取100名學生的筆試成績,按成績共分五組,得到頻率分布表如下表所示。
| 組號 | 分組 | 頻數 | 頻率 |
| 第一組 | [160,165) | 5 | 0.05 |
| 第二組 | [165,170) | 35 | 0.35 |
| 第三組 | [170,175) | 30 | a |
| 第四組 | [175,180) | b | 0.2 |
| 第五組 | [180,185) | 10 | 0.1 |
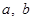 的值;
的值; 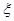 ,求
,求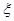 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
甲、乙兩位籃球運動員進行定點投籃,甲投籃一次命中的概率為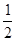 ,乙投籃一次命中的概率為
,乙投籃一次命中的概率為 .每人各投4個球,兩人投籃命中的概率互不影響.
.每人各投4個球,兩人投籃命中的概率互不影響.
(1)求甲至多命中1個球且乙至少命中1個球的概率;
(2)若規定每投籃一次命中得3分,未命中得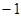 分,求乙所得分數
分,求乙所得分數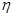 的概率分布和數學期望.
的概率分布和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com