
某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的50位顧客的相關數據,如下表所示:
一次購物量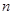 (件) (件) | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顧客數(人) |  | 20 | 10 | 5 | 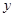 |
| 結算時間(分鐘/人) | 0.5 | 1 | 1.5 | 2 | 2.5 |
 與
與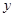 的值;
的值; 的分布列與數學期望;
的分布列與數學期望;(1)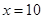 ,
,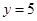 ;(2)詳見解析;(3)
;(2)詳見解析;(3)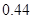 .
.
解析試題分析:(1)先根據“這50位顧客中一次購物量少于10件的顧客占80%”這一條件求出 的值,然后再根據余下的人數占總人數的
的值,然后再根據余下的人數占總人數的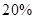 求出
求出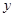 的值;(2)先確定一次購物時間所對應的顧客數,并計算出相應的概率,然后再列出隨機變量的分布列并計算數學期望;(3)先確定2位顧客需結算時間總和不超過2分鐘的不同組合,并結合獨立事件的概率進行計算即可.
的值;(2)先確定一次購物時間所對應的顧客數,并計算出相應的概率,然后再列出隨機變量的分布列并計算數學期望;(3)先確定2位顧客需結算時間總和不超過2分鐘的不同組合,并結合獨立事件的概率進行計算即可.
試題解析:(1)依題意得,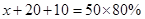 ,
, ,解得
,解得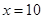 ,
,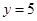 .
.
(2)該超市所有顧客一次購物的結算時間組成一個總體,所以收集的50位顧客一次購物的結算時間可視為總體的一個容量為50的隨機樣本,將頻率視為概率得,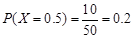 ,
,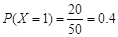 ,
, ,
,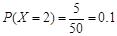 ,
,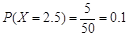 .
.
所以 的分布列為
的分布列為
0.5 1 1.5 2 2.5 
0.2 0.4 0.2 0.1 0.1  的數學期望為
的數學期望為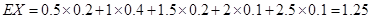 .
.
(3)記“該顧客結算前的等候時間不超過2分鐘”為事件A,該顧客前面第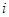 位顧客的結算時間為
位顧客的結算時間為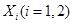 ,由于各顧客的結算相互獨立,且
,由于各顧客的結算相互獨立,且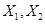 的分布列都與
的分布列都與 的分布列相同,所以
的分布列相同,所以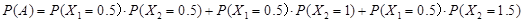
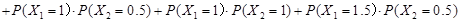
 為所求.
為所求.
考點:離散型隨機變量及其分布列、獨立事件的概率


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
在一個盒子里裝有4枝圓珠筆,其中3枝一等品,1枝三等品
(1)從盒子里任取2枝恰有1枝三等品的概率多大?
(2)從盒子里第一次任取1枝(不放回),第二次任取1枝;第一次取的是三等品,第二次取的是一等品的概率有多大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某旅游公司提供甲、乙、丙三處旅游景點,游客選擇游玩哪個景點互不影響,已知某游客選擇游甲地而不選擇游乙地和丙地的概率為0.08,選擇游甲地和乙地而不選擇游丙地的概率為0.12,在甲、乙、丙三處旅游景點中至少選擇游一個景點0.88,用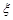 表示游客在甲、乙、丙三處旅游景點中選擇游玩的景點數和沒有選擇游玩的景點數的乘積.
表示游客在甲、乙、丙三處旅游景點中選擇游玩的景點數和沒有選擇游玩的景點數的乘積.
(Ⅰ)記“函數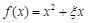 是R上的偶函數”為事件A,求事件A的概率;
是R上的偶函數”為事件A,求事件A的概率;
(Ⅱ)求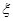 的概率分布列及數學期望.
的概率分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解甲、乙兩廠產品的質量,從兩廠生產的產品中分別隨機抽取各10件樣品,測量產品中某種元素的含量(單位:毫克).如圖是測量數據的莖葉圖: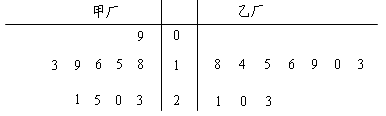
規定:當產品中的此種元素含量不小于18毫克時,該產品為優等品.
(1)試用上述樣本數據估計甲、乙兩廠生產的優等品率;
(2)從乙廠抽出的上述10件樣品中,隨機抽取3件,求抽到的3件樣品中優等品數 的分布列及其數學期望
的分布列及其數學期望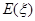 ;
;
(3)從甲廠的10件樣品中有放回的隨機抽取3件,也從乙廠的10件樣品中有放回的隨機抽取3件,求抽到的優等品數甲廠恰比乙廠多2件的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在兩個不同的口袋中,各裝有大小、形狀完全相同的1個紅球、2個黃球.現分別從每一個口袋中各任取2個球,設隨機變量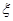 為取得紅球的個數.
為取得紅球的個數.
(Ⅰ)求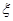 的分布列;
的分布列;
(Ⅱ)求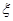 的數學期望
的數學期望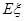 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校學習小組開展“學生語文成績與外語成績的關系”的課題研究,對該校高二年級800名學生上學期期末語文和外語成績,按優秀和不優秀分類得結果:語文和外語都優秀的有60人,語文成績優秀但外語不優秀的有140人,外語成績優秀但語文不優秀的有100人.
(Ⅰ)能否在犯錯概率不超過0.001的前提下認為該校學生的語文成績與外語成績有關系?
(Ⅱ)將上述調查所得到的頻率視為概率,從該校高二年級學生成績中,有放回地隨機抽取3名學生的成績,記抽取的3 個成績中語文,外語兩科成績至少有一科優秀的個數為X ,求X的分布列和期望E(x).
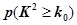 | 0.010 | 0.005 | 0.001 |
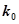 | 6.635 | 7.879 | 10.828 |
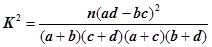
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
福彩中心發行彩票的目的是為了獲取資金資助福利事業,現在福彩中心準備發行一種面值為5元的福利彩票刮刮卡,設計方案如下:(1)該福利彩票中獎率為50%;(2)每張中獎彩票的中獎獎金有5元,50元和150元三種;(3)顧客購買一張彩票獲得150元獎金的概率為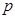 ,獲得50元獎金的概率為
,獲得50元獎金的概率為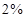 .
.
(I)假設某顧客一次性花10元購買兩張彩票,求其至少有一張彩票中獎的概率;
(II)為了能夠籌得資金資助福利事業, 求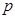 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某車間共有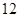 名工人,隨機抽取
名工人,隨機抽取 名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數. 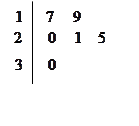
(Ⅰ) 根據莖葉圖計算樣本均值;
(Ⅱ) 日加工零件個數大于樣本均值的工人為優秀工人,根據莖葉圖推斷該車間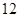 名工人中有幾名優秀工人;
名工人中有幾名優秀工人;
(Ⅲ) 從該車間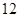 名工人中,任取
名工人中,任取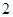 人,求恰有
人,求恰有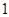 名優秀工人的概率.
名優秀工人的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com