
【題目】已知函數![]() ,
, ![]() .
.
(1)判斷函數![]() 是否有零點;
是否有零點;
(2)設函數![]() ,若
,若![]() 在
在![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)函數![]() 有零點(2)
有零點(2)![]() 或
或![]()
【解析】試題分析:(1)由函數f(x)=mx+3,g(x)=x2+2x+m,我們易給出函數f(x)﹣g(x)的零點,判斷對應方程的△與0的關系,易得結論;
(2)由函數f(x)=mx+3,g(x)=x2+2x+m,我們易給出函數G(x)=f(x)﹣g(x)﹣1,若|G(x)|在[﹣1,0]上是減函數,根據對折變換函數圖象的特征,我們分△≤0和△>0兩種情況進行討論,可得到滿足條件的m的取值范圍.
試題解析:
(1)![]() ,
,
則![]() ,
,
故函數![]() 有零點;
有零點;
(2)![]() ,
,
![]() ,
,
①當![]() ,即
,即![]() 時,
時, ![]() ,
,
若![]() 在
在![]() 上是減函數,則
上是減函數,則![]() ,即
,即![]() ,
,
即![]() 時,符合條件,
時,符合條件,
② 當![]() ,即
,即![]() 或
或![]() 時,
時,
若![]() ,則
,則![]() ,要使
,要使![]() 在
在![]() 上是減函數,則
上是減函數,則![]() ,
, ![]() ,
,
若![]() ,則
,則![]() ,顯然
,顯然![]() 在
在![]() 上是減函數,則
上是減函數,則![]() .
.
綜上, ![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 及圓
及圓![]() :
: ![]() .
.
(1)若直線![]() 過點
過點![]() 且與圓心
且與圓心![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 的方程.
的方程.
(2)設直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點,是否存在實數
兩點,是否存在實數![]() ,使得過點
,使得過點![]() 的直線
的直線![]() 垂直平分弦
垂直平分弦![]() ?若存在,求出實數
?若存在,求出實數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a , b , c是正整數,且a∈[70,80),b∈[80,90),c∈[90,100],當數據a , b , c的方差最小時,a+b+c的值為( )
A.252或253
B.253或254
C.254或255
D.267或268
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 滿足:在定義域
滿足:在定義域![]() 內存在實數
內存在實數![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 為“
為“![]() 的飽和函數”.給出下列四個函數:①
的飽和函數”.給出下列四個函數:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() .其中是“
.其中是“![]() 的飽和函數”的所有函數的序號是______________.
的飽和函數”的所有函數的序號是______________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線 ![]() 在
在 ![]() 的上方,且曲線
的上方,且曲線 ![]() 上的任意一點到點
上的任意一點到點 ![]() 的距離比到直線
的距離比到直線 ![]() 的距離都小1.
的距離都小1.
(Ⅰ)求曲線 ![]() 的方程;
的方程;
(Ⅱ)設 ![]() ,過點
,過點 ![]() 的直線與曲線
的直線與曲線 ![]() 相交于
相交于 ![]() 兩點.
兩點.
①若 ![]() 是等邊三角形,求實數
是等邊三角形,求實數 ![]() 的值;
的值;
②若 ![]() ,求實數
,求實數 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上存在導數f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(6﹣m)﹣f(m)﹣18+6m≥0,則實數m的取值范圍為( )
A.[﹣3,3]
B.[3,+∞)
C.[2,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國個人所得稅》規定,公民月工資、薪金所得不超過3500元的部分不納稅,超過3500元的部分為全月納稅所得額,此項稅款按下表分段累計計算:

已知張先生的月工資、薪金所得為10000元,問他當月應繳納多少個人所得稅?
設王先生的月工資、薪金所得為![]() 元,當月應繳納個人所得稅為
元,當月應繳納個人所得稅為![]() 元,寫出
元,寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)已知王先生一月份應繳納個人所得稅為303元,那么他當月的個工資、薪金所得為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知首項為 ![]() 的等比數列{an}不是遞減數列,其前n項和為Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差數列.
的等比數列{an}不是遞減數列,其前n項和為Sn (n∈N*),且S3+a3 , S5+a5 , S4+a4成等差數列.
(1)求數列{an}的通項公式;
(2)若實數a使得a>Sn+ ![]() 對任意n∈N*恒成立,求a的取值范圍.
對任意n∈N*恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F為雙曲線 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )
=1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )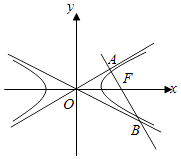
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com