
【題目】若函數![]() 滿足:在定義域
滿足:在定義域![]() 內存在實數
內存在實數![]() ,使得
,使得![]() 成立,則稱函數
成立,則稱函數![]() 為“
為“![]() 的飽和函數”.給出下列四個函數:①
的飽和函數”.給出下列四個函數:①![]() ;②
;②![]() ; ③
; ③![]() ;④
;④![]() .其中是“
.其中是“![]() 的飽和函數”的所有函數的序號是______________.
的飽和函數”的所有函數的序號是______________.
【答案】②④
【解析】①f(x)=![]() ,D=(﹣∞,0)∪(0,+∞),
,D=(﹣∞,0)∪(0,+∞),
若f(x)=![]() 是“1的飽和函數”,
是“1的飽和函數”,
則存在非零實數x0,使得![]() =
=![]() ,
,
即x02+x0+1=0,
因為此方程無實數解,
所以函數f(x)=![]() 不是“1的飽和函數”.
不是“1的飽和函數”.
②f(x)=2x,D=R,則存在實數x0,使得2x0+1=2x0+2,解得x0=1,
因為此方程有實數解,
所以函數f(x)=2x是“1的飽和函數”.
③f(x)=lg(x2+2),若存在x,使f(x+1)=f(x)+f(1)
則lg[(x+1)2+2]=lg(x2+2)+lg3
即2x2﹣2x+3=0,
∵△=4﹣24=﹣20<0,故方程無解.
即f(x)=lg(x2+2)不是“1的飽和函數”.
④f(x)=cosπx,存在x=![]() ,使得f(x+1)=f(x)+f(1),
,使得f(x+1)=f(x)+f(1),
即f(x)=cosπx是“1的飽和函數”.
故答案為:②④.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓 ![]() +
+ ![]() =1(a>b>0)的離心率為e,D為右準線上一點.
=1(a>b>0)的離心率為e,D為右準線上一點.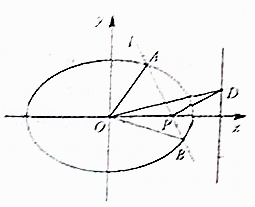
(1)若e= ![]() ,點D的橫坐標為4,求橢圓的方程;
,點D的橫坐標為4,求橢圓的方程;
(2)設斜率存在的直線l經過點P( ![]() ,0),且與橢圓交于A,B兩點.若
,0),且與橢圓交于A,B兩點.若 ![]() +
+ ![]() =
= ![]() ,DP⊥l,求橢圓離心率e.
,DP⊥l,求橢圓離心率e.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某社區中學生的課外活動,對該社區的100名中學生進行了調研,隨機抽取了若干名,年齡全部介于13與18之間,將年齡按如下方式分成五組:第一組![]() ;第二組
;第二組![]() ;第五組
;第五組![]() .按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三個組的頻率之比為
.按上述分組方法得到的頻率分布直方圖如圖所示,已知圖中從左到右的前三個組的頻率之比為![]() ,且第二組的頻數為4.
,且第二組的頻數為4.
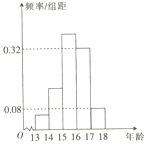
(1)試估計這100名中學生中年齡在![]() 內的人數;
內的人數;
(2)求調研中隨機抽取的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在D上的函數 ![]() ,若滿足:
,若滿足: ![]() ,都有
,都有 ![]() 成立,則稱
成立,則稱 ![]() 是D上的有界函數,其中M稱為函數
是D上的有界函數,其中M稱為函數 ![]() 的上界.
的上界.
(I)設 ![]() ,證明:
,證明: ![]() 在
在 ![]() 上是有界函數,并寫出
上是有界函數,并寫出 ![]() 所有上界的值的集合;
所有上界的值的集合;
(II)若函數 ![]() 在
在 ![]() 上是以3為上界的有界函數,求實數a的取值范圍.
上是以3為上界的有界函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρ2(1+3sin2θ)=4,曲線C2: ![]() (θ為參數).
(θ為參數).
(Ⅰ)求曲線C1的直角坐標方程和C2的普通方程;
(Ⅱ)極坐標系中兩點A(ρ1 , θ0),B(ρ2 , θ0+ ![]() )都在曲線C1上,求
)都在曲線C1上,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)用五點法畫出它在一個周期內的閉區間上的圖象;
(2)指出f(x)的周期、振幅、初相、對稱軸;
(3)此函數圖象由y=sinx的圖象怎樣變換得到?(注:y軸上每一豎格長為1)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com