
【題目】設(shè)函數(shù)f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.
)=0.
(Ⅰ)求ω;
(Ⅱ)將函數(shù)y=f(x)的圖象上各點(diǎn)的橫坐標(biāo)伸長為原來的2倍(縱坐標(biāo)不變),再將得到的圖象向左平移 ![]() 個(gè)單位,得到函數(shù)y=g(x)的圖象,求g(x)在[﹣
個(gè)單位,得到函數(shù)y=g(x)的圖象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
【答案】解:(Ⅰ)函數(shù)f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() )
)
=sinωxcos ![]() ﹣cosωxsin
﹣cosωxsin ![]() ﹣sin(
﹣sin( ![]() ﹣ωx)
﹣ωx)
= ![]() sinωx﹣
sinωx﹣ ![]() cosωx
cosωx
= ![]() sin(ωx﹣
sin(ωx﹣ ![]() ),
),
又f( ![]() )=
)= ![]() sin(
sin( ![]() ω﹣
ω﹣ ![]() )=0,
)=0,
∴ ![]() ω﹣
ω﹣ ![]() =kπ,k∈Z,
=kπ,k∈Z,
解得ω=6k+2,
又0<ω<3,
∴ω=2;
(Ⅱ)由(Ⅰ)知,f(x)= ![]() sin(2x﹣
sin(2x﹣ ![]() ),
),
將函數(shù)y=f(x)的圖象上各點(diǎn)的橫坐標(biāo)伸長為原來的2倍(縱坐標(biāo)不變),得到函數(shù)y= ![]() sin(x﹣
sin(x﹣ ![]() )的圖象;
)的圖象;
再將得到的圖象向左平移 ![]() 個(gè)單位,得到y(tǒng)=
個(gè)單位,得到y(tǒng)= ![]() sin(x+
sin(x+ ![]() ﹣
﹣ ![]() )的圖象,
)的圖象,
∴函數(shù)y=g(x)= ![]() sin(x﹣
sin(x﹣ ![]() );
);
當(dāng)x∈[﹣ ![]() ,
, ![]() ]時(shí),x﹣
]時(shí),x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
∴當(dāng)x=﹣ ![]() 時(shí),g(x)取得最小值是﹣
時(shí),g(x)取得最小值是﹣ ![]() ×
× ![]() =﹣
=﹣ ![]() .
.
【解析】(1)根據(jù)兩角和的正弦公式可得到f(x)=![]() sin(ωx﹣
sin(ωx﹣ ![]() ),且f(
),且f(![]() )=0,即可得到ω=2,(2)根據(jù)三角函數(shù)圖象平移的規(guī)則(左加右減)可得到g(x)的解析式,由三角函數(shù)的圖象和性質(zhì)可得出g(x)的最小值.
)=0,即可得到ω=2,(2)根據(jù)三角函數(shù)圖象平移的規(guī)則(左加右減)可得到g(x)的解析式,由三角函數(shù)的圖象和性質(zhì)可得出g(x)的最小值.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)列{an}的前n項(xiàng)和記為Sn , a1=2,an+1=Sn+2(n∈N*).
(Ⅰ)求{an}的通項(xiàng)公式;
(Ⅱ)求數(shù)列{nan}的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 在區(qū)間
在區(qū)間![]() 上的值域
上的值域![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)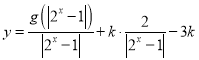 有三個(gè)零點(diǎn),求實(shí)數(shù)
有三個(gè)零點(diǎn),求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為增強(qiáng)市民的節(jié)能環(huán)保意識(shí),某市面向全市征召義務(wù)宣傳志愿者.從符合條件的500名志愿者中隨機(jī)抽取100名志愿者,其年齡頻率分布直方圖如圖所示,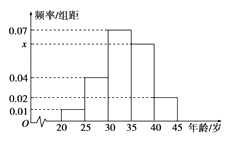
(1)求圖中 ![]() 的值并根據(jù)頻率分布直方圖估計(jì)這500名志愿者中年齡在
的值并根據(jù)頻率分布直方圖估計(jì)這500名志愿者中年齡在 ![]() 歲的人數(shù);
歲的人數(shù);
(2)在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取20名參加中心廣場的宣傳活動(dòng),再從這20名中采用簡單隨機(jī)抽樣方法選取3名志愿者擔(dān)任主要負(fù)責(zé)人.記這3名志愿者中“年齡低于35歲”的人數(shù)為 ![]() ,求
,求 ![]() 的分布列及均值.
的分布列及均值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】△ABC的內(nèi)角A,B,C所對(duì)的邊分別為a,b,c,已知2c﹣a=2bcosA.
(1)求角B的大小;
(2)若 ![]() ,求a+c的最大值.
,求a+c的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間的一臺(tái)機(jī)床生產(chǎn)出一批零件,現(xiàn)從中抽取8件,將其編為![]() ,
, ![]() ,…,
,…, ![]() ,測量其長度(單位:
,測量其長度(單位: ![]() ),得到如表中數(shù)據(jù):
),得到如表中數(shù)據(jù):
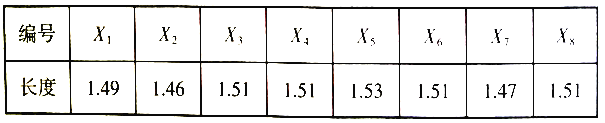
其中長度在區(qū)間![]() 內(nèi)的零件為一等品.
內(nèi)的零件為一等品.
(1)從上述8個(gè)零件中,隨機(jī)抽取一個(gè),求這個(gè)零件為一等品的概率;
(2)從一等品零件中,隨機(jī)抽取3個(gè).
①用零件的編號(hào)列出所有可能的抽取結(jié)果;
②求這3個(gè)零件長度相等的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 底面
底面![]() ,且
,且![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 在
在![]() 上,且
上,且![]() .
.
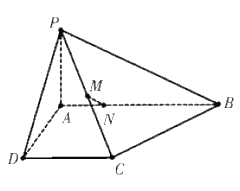
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓E: ![]() 的左、右焦點(diǎn)分別為F1、F2 , 離心率
的左、右焦點(diǎn)分別為F1、F2 , 離心率 ![]() ,P為橢圓E上的任意一點(diǎn)(不含長軸端點(diǎn)),且△PF1F2面積的最大值為1.
,P為橢圓E上的任意一點(diǎn)(不含長軸端點(diǎn)),且△PF1F2面積的最大值為1.
(Ⅰ)求橢圓E的方程;
(Ⅱ)已知直x﹣y+m=0與橢圓E交于不同的兩點(diǎn)A,B,且線AB的中點(diǎn)不在圓 ![]() 內(nèi),求m的取值范圍.
內(nèi),求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知在多面體ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F(xiàn)為CE的中點(diǎn).
(1)求直線AF與平面ACD所成的角;
(2)求證:平面BCE⊥平面DCE.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com