Question

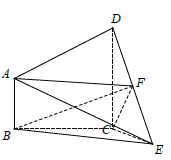
【題目】如圖，在四棱錐中， , ，點為棱的中點.

（1）證明： 平面；

（2）若，求三棱錐的體積.

Answer 1

【答案】（1）見解析（2）

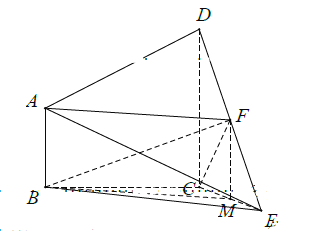
【解析】試題分析：（1）取的中點，連接，根據三角形中位線定理可得，從而可得四邊形為平行四邊形， ，利用線面平行的判定定理可得平面；（2）由得，由勾股定理可得，從而得平面， 到平面的距離為，利用三角形面積公式求出底面積，根據等積變換及棱錐的體積公式可得 .

試題解析：（1）取的中點，連接.

因為點為棱的中點，

所以且，

因為且 ，

所以且，

所以四邊形為平行四邊形，

所以，

因為平面， 平面，

所以平面.

（2）因為，

所以.

因為，所以，

所以，

因為, 平面， 平面,

所以平面.

因為點為棱的中點，且，

所以點到平面的距離為2.

.

三棱錐的體積 .

【方法點晴】本題主要考查線面平行的判定定理、利用等積變換求三棱錐體積，屬于中檔題. 證明線面平行的常用方法：①利用線面平行的判定定理，使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線，可利用幾何體的特征，合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質，即兩平面平行，在其中一平面內的直線平行于另一平面. 本題（1）是就是利用方法①證明的.