
【題目】在校運動會上,甲、乙、丙三位同學每人均從跳遠,跳高,鉛球,標槍四個項目中隨機選一項參加比賽,假設三人選項目時互不影響,且每人選每一個項目時都是等可能的
(1)求僅有兩人所選項目相同的概率;
(2)設X為甲、乙、丙三位同學中選跳遠項目的人數,求X的分布列和數學期望E(X)
【答案】
(1)解:甲、乙、丙三位同學每人均從跳遠,跳高,鉛球,標槍四個項目中隨機選一項參加比賽,
假設三人選項目時互不影響,且每人選每一個項目時都是等可能的,
基本事件總數n=43=64,
僅有兩人所選項目相同包含的基本事件個數m=C ![]() =36,
=36,
∴僅有兩人所選項目相同的概率p= ![]() =
= ![]()
(2)解:由題意X的可能取值為0,1,2,3,
P(X=0)= ![]() =
= ![]() ,
,
P(X=1)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=3)= ![]() =
= ![]() ,
,
∴X的分布列為:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
EX= ![]() =
= ![]()
【解析】(1)先求出基本事件總數n=43=64,再求出僅有兩人所選項目相同包含的基本事件個數m=C ![]() =36,由此能求出僅有兩人所選項目相同的概率.(2)由題意X的可能取值為0,1,2,3,分別求出相應的概率,由此能求出X的分布列和數學期望.
=36,由此能求出僅有兩人所選項目相同的概率.(2)由題意X的可能取值為0,1,2,3,分別求出相應的概率,由此能求出X的分布列和數學期望.
【考點精析】通過靈活運用離散型隨機變量及其分布列,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列即可以解答此題.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:高中數學 來源: 題型:
【題目】如圖所示的是某池塘中的浮萍蔓延的面積![]() 與時間
與時間![]() 月)的關系
月)的關系![]() 有以下敘述:
有以下敘述:
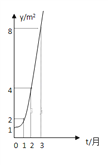
①這個指數函數的底數是2;
②第5個月時,浮萍的面積就會超過![]()
③浮萍從![]() 蔓延到
蔓延到![]() 需要經過1.5個月;
需要經過1.5個月;
④浮萍每個月增加的面積都相等;
⑤若浮萍蔓延到![]() 所經過的時間分別為
所經過的時間分別為![]() 則
則![]() .其中正確的是
.其中正確的是
A. ①② B. ①②③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R的函數![]() 是偶函數,且滿足
是偶函數,且滿足![]() 上的解析式為
上的解析式為![]() ,過點
,過點![]() 作斜率為k的直線l,若直線l與函數
作斜率為k的直線l,若直線l與函數![]() 的圖象至少有4個公共點,則實數k的取值范圍是
的圖象至少有4個公共點,則實數k的取值范圍是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖(甲),在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 的中點,現將
的中點,現將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如圖(乙).
,如圖(乙).
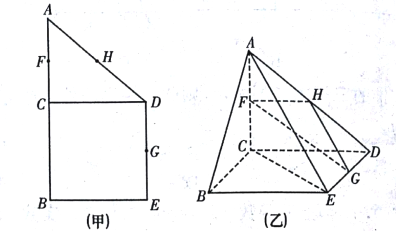
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,半圓AOB是某市休閑廣場的平面示意圖,半徑OA的長為10,管理部門在A,B兩處各安裝好一個光源,其相應的光強度分別為4和9,根據光學原理,地面上某處照度y與光強度I成正比,與光源距離x的平方成反比,即y= ![]() (k為比例系數),經測量,在弧AB的中心C處的照度為130.(C處的照度為A,B兩處光源的照度之和)
(k為比例系數),經測量,在弧AB的中心C處的照度為130.(C處的照度為A,B兩處光源的照度之和) 
(1)求比例系數k的值;
(2)現在管理部門計劃在半圓弧AB上,照度最小處增設一個光源P,試問新增光源P安裝在什么位置?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某港口水的深度![]() 是時間
是時間![]() ,單位:
,單位: ![]() 的函數,記作
的函數,記作![]() .下面是某日水深的數據:
.下面是某日水深的數據:

經長期觀察, ![]() 的曲線可以近似地看成函數
的曲線可以近似地看成函數![]() 的圖象.一般情況下,船舶航行時,船底離海底的距離為
的圖象.一般情況下,船舶航行時,船底離海底的距離為![]() 或
或![]() 以上時認為是安全的(船舶停靠時,船底只需不碰海底即可).
以上時認為是安全的(船舶停靠時,船底只需不碰海底即可).
(1)求![]() 與
與![]() 滿足的函數關系式;
滿足的函數關系式;
(2)某船吃水程度(船底離水面的距離)為![]() ,如果該船希望在同一天內安全進出港,請問它同一天內最多能在港內停留多少小時?(忽略進出港所需的時間).
,如果該船希望在同一天內安全進出港,請問它同一天內最多能在港內停留多少小時?(忽略進出港所需的時間).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com