
【題目】已知數列![]() 滿足a1=2,an+1=3an+2,
滿足a1=2,an+1=3an+2,
(1)證明:![]() 是等比數列,并求
是等比數列,并求![]() 的通項公式;
的通項公式;
(2)證明: ![]() .
.
【答案】(1)證明見解析,![]() ;(2)證明見解析。
;(2)證明見解析。
【解析】
(1)要證明數列![]() 是等比數列,應在an+1=3an+2中找到數列
是等比數列,應在an+1=3an+2中找到數列![]() 中兩項之間的關系,用等比數列定義可證數列
中兩項之間的關系,用等比數列定義可證數列![]() 是等比數列。用等比數列的通項公式可得數列
是等比數列。用等比數列的通項公式可得數列![]() 的通項公式,進而可得
的通項公式,進而可得![]() 的通項公式。(2)由(1)可知
的通項公式。(2)由(1)可知![]() ,可知數列
,可知數列![]() 既不是等差數列也不是等比數列,所以用放縮法可得
既不是等差數列也不是等比數列,所以用放縮法可得![]() ≤
≤![]() ,進而可得
,進而可得![]() +
+![]() +…+
+…+![]() ≤
≤![]() (1+
(1+![]() +…+
+…+![]() ),根據等比數列前n項和公式求和,即可證得結論。
),根據等比數列前n項和公式求和,即可證得結論。
(1)證明:由an+1=3an+2,
得an+1+1=3![]() .
.
又a1+1=3,
所以![]() 是首項為3,公比為3的等比數列.
是首項為3,公比為3的等比數列.
∴an+1=![]() ,
,
因此{an}的通項公式為an=![]()
(2)解: 由(1)知![]() ,
,
因為當n≥1時,3n-1≥2×3n-1,
所以![]() ≤
≤![]()
于是![]() +
+![]() +…+
+…+![]() ≤
≤![]() (1+
(1+![]() +…+
+…+![]() )=
)=![]()
![]() <
<![]() .
.
所以![]() +
+![]() +…+
+…+![]() <
<![]() .
.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:高中數學 來源: 題型:
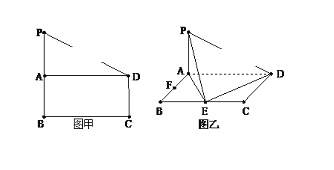
【題目】如圖甲,在直角梯形PBCD中,PB∥CD,CD⊥BC,BC=PB=2CD,A是PB的中點.
現沿AD把平面PAD折起,使得PA⊥AB(如圖乙所示),E、F分別為BC、AB邊的中點.
(1)求證:平面PAE⊥平面PDE;
(2)在PE上找一點Q,使得平面BDQ⊥平面ABCD.
(3)在PA上找一點G,使得FG∥平面PDE.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在下列結論中:
①若向量![]() 共線,則向量
共線,則向量![]() 所在的直線平行;
所在的直線平行;
②若向量![]() 所在的直線為異面直線,則向量
所在的直線為異面直線,則向量![]() 一定不共面;
一定不共面;
③若三個向量![]() 兩兩共面,則向量
兩兩共面,則向量![]() 共面;
共面;
④已知空間的三個向量![]() ,則對于空間的任意一個向量
,則對于空間的任意一個向量![]() 總存在實數x,y,z使得
總存在實數x,y,z使得![]() .
.
其中正確結論的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,曲線f(x)=
,曲線f(x)= ![]() 在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數的底數) (Ⅰ)若函數f(x)在區間(m,m+1)上存在極值,求實數m的取值范圍;
在點(e,f(e))處的切線與直線e2x﹣y+e=0垂直.(注:e為自然對數的底數) (Ⅰ)若函數f(x)在區間(m,m+1)上存在極值,求實數m的取值范圍;
(Ⅱ)求證:當x>1時, ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,ABC﹣A1B1C1是底面邊長為2,高為 ![]() 的正三棱柱,經過AB的截面與上底面相交于PQ,設C1P=λC1A1(0<λ<1).、
的正三棱柱,經過AB的截面與上底面相交于PQ,設C1P=λC1A1(0<λ<1).、 
(1)證明:PQ∥A1B1;
(2)當 ![]() 時,求點C到平面APQB的距離.
時,求點C到平面APQB的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A={x|﹣1≤x≤2},B={x|x2﹣x+(m﹣m2)<0}.
(1)當m< ![]() 時,化簡集合B;
時,化簡集合B;
(2)p:x∈A,命題q:x∈B,且命題p是命題q的必要不充分條件,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)平面直角坐標系xoy中,直線![]() 截以原點O為圓心的圓所得的弦長為
截以原點O為圓心的圓所得的弦長為![]()
(1)求圓O的方程;
(2)若直線![]() 與圓O切于第一象限,且與坐標軸交于D,E,當DE長最小時,求直線
與圓O切于第一象限,且與坐標軸交于D,E,當DE長最小時,求直線![]() 的方程;
的方程;
(3)設M,P是圓O上任意兩點,點M關于x軸的對稱點為N,若直線MP、NP分別交于x軸于點(m,0)和(n,0),問mn是否為定值?若是,請求出該定值;若不是,請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com