
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過右焦點F的直線l與C相交于A、B兩點,當l的斜率為1時,坐標原點O到l的距離為2。
,過右焦點F的直線l與C相交于A、B兩點,當l的斜率為1時,坐標原點O到l的距離為2。
(1)求橢圓C的方程;
(2)橢圓C上是否存在一點P,使得當l繞F轉到某一位置時,有![]() 成立?若存在,求點P的坐標與直線l的方程;若不存在,說明理由。
成立?若存在,求點P的坐標與直線l的方程;若不存在,說明理由。
【答案】(1)![]() ; (2)
; (2)![]() ,直線
,直線![]() ,或
,或![]() ,直線
,直線![]() .
.
【解析】
(1) 設![]() ,可得直線l的方程為
,可得直線l的方程為![]() ,運用點到直線距離公式,可求出c,再由離心率公式即可求出a,b從而可得橢圓方程;
,運用點到直線距離公式,可求出c,再由離心率公式即可求出a,b從而可得橢圓方程;
(2) 設![]() ,
,![]() ,
,![]() , 設
, 設![]() 代入橢圓方程消元,再由韋達定理和向量的坐標運算,求出點P的坐標,代入橢圓方程,即可求出結果.
代入橢圓方程消元,再由韋達定理和向量的坐標運算,求出點P的坐標,代入橢圓方程,即可求出結果.
(1)設![]() ,可得直線l的方程為
,可得直線l的方程為![]() ,
,
即為![]() ,由坐標原點O到l的距離為2,
,由坐標原點O到l的距離為2,
即有![]() ,解得
,解得![]() ,
,
由![]() ,可得
,可得![]() ,b=2,
,b=2,
即有橢圓的方程為![]() ;
;
(2)設![]() ,
,![]() ,
,![]() ,
,
①當直線![]() 的斜率存在,設其方程為:
的斜率存在,設其方程為:![]()
由![]() ,消去y得
,消去y得![]() .
.
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
將P點坐標代入橢圓得![]() ,
,
∴![]() ,∴
,∴![]() (
(![]() 舍去),即為
舍去),即為![]() .
.
當![]() 時,
時,![]() ,直線
,直線![]() ,
,
當![]() 時,
時,![]() ,直線
,直線![]() .
.
②當直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為:
的方程為:![]() ,
,
依題意,四邊形OAPB為菱形,此時點P不在橢圓上,
即當直線![]() 的斜率不存在時,不適合題意;
的斜率不存在時,不適合題意;
綜上所述,存在P,且![]() ,直線
,直線![]() ,
,
或![]() ,直線
,直線![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖是一個幾何體的平面展開圖,其中四邊形ABCD為正方形,△PDC, △PBC, △PAB, △PDA為全等的等邊三角形,E、F分別為PA、PD的中點,在此幾何體中,下列結論中錯誤的為 ( )

A. 平面BCD⊥平面PAD B. 直線BE與直線AF是異面直線
C. 直線BE與直線CF共面 D. 面PAD與面PBC的交線與BC平行
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為弘揚優良傳統,展示80年來的辦學成果,特舉辦“建校80周年教育成果展示月”活動。現在需要招募活動開幕式的志愿者,在眾多候選人中選取100名志愿者,為了在志愿者中選拔出節目主持人,現按身高分組,得到的頻率分布表如圖所示.


(1)請補充頻率分布表中空白位置相應數據,再在答題紙上完成下列頻率分布直方圖;
(2)為選拔出主持人,決定在第3、4、5組中用分層抽樣抽取6人上臺,求第3、4、5組每組各抽取多少人?
(3)在(2)的前提下,主持人會在上臺的6人中隨機抽取2人表演詩歌朗誦,求第3組至少有一人被抽取的概率?
參考公式:
 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,兩條準線之間的距離為
,兩條準線之間的距離為![]() .
.
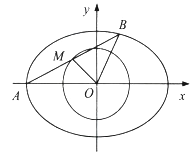
(1)求橢圓的標準方程;
(2)已知橢圓的左頂點為![]() ,點
,點![]() 在圓
在圓![]() 上,直線
上,直線![]() 與橢圓相交于另一點
與橢圓相交于另一點![]() ,且
,且![]() 的面積是
的面積是![]() 的面積的
的面積的![]() 倍,求直線
倍,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若數列![]() 同時滿足:①對于任意的正整數
同時滿足:①對于任意的正整數![]() ,
, ![]() 恒成立;②對于給定的正整數
恒成立;②對于給定的正整數![]() ,
, ![]() 對于任意的正整數
對于任意的正整數![]() 恒成立,則稱數列
恒成立,則稱數列![]() 是“
是“![]() 數列”.
數列”.
(1)已知![]() 判斷數列
判斷數列![]() 是否為“
是否為“![]() 數列”,并說明理由;
數列”,并說明理由;
(2)已知數列![]() 是“
是“![]() 數列”,且存在整數
數列”,且存在整數![]() ,使得
,使得![]() ,
, ![]() ,
, ![]() ,
, ![]() 成等差數列,證明:
成等差數列,證明: ![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】潮州統計局就某地居民的月收入調查了![]() 人,并根據所得數據畫了樣本的頻率分
人,并根據所得數據畫了樣本的頻率分
布直方圖(每個分組包括左端點,不包括右端點,如第一組表示收入在![]() )。
)。

(1)求居民月收入在![]() 的頻率;
的頻率;
(2)根據頻率分布直方圖算出樣本數據的中位數;
(3)為了分析居民的收入與年齡、職業等方面的關系,必須按月收入再從這![]() 人中分層抽樣方法抽出
人中分層抽樣方法抽出![]() 人作進一步分析,則月收入在
人作進一步分析,則月收入在![]() 的這段應抽多少人?
的這段應抽多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 與曲線
與曲線![]() 的直角坐標方程:
的直角坐標方程:
(Ⅱ)過點![]() 平行于直線
平行于直線![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 軌跡的直角坐標方程.
軌跡的直角坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com