
【題目】已知橢圓![]() :
:![]()
![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且過點
的焦點重合,且過點![]() .過點
.過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,
兩點, ![]() 為橢圓的左頂點.
為橢圓的左頂點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求![]() 面積的最大值,并求此時直線
面積的最大值,并求此時直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直線l的方程為x=1.
;(2)直線l的方程為x=1.
【解析】試題分析:(1)利用橢圓和拋物線有一個公共焦點和點在橢圓上進行求解;(2) 聯(lián)立直線和橢圓的方程,得到關于![]() 的一元二次方程,再利用根與系數的關系、弦長公式和基本不等式進行求解.
的一元二次方程,再利用根與系數的關系、弦長公式和基本不等式進行求解.
試題解析:(1)因為拋物線y2=4![]() x的焦點為(
x的焦點為(![]() ,0),所以橢圓C的半焦距c=
,0),所以橢圓C的半焦距c=![]() ,即a2-b2=3. ①
,即a2-b2=3. ①
把點Q![]() 代入
代入![]() +
+![]() =1,得
=1,得![]() +
+![]() =1. ②
=1. ②
由①②解得a2=4,b2=1.所以橢圓C的標準方程為![]() +y2=1.
+y2=1.
(2)設直線l的方程為x=ty+1,代入![]() +y2=1,
+y2=1,
得(t2+4)y2+2ty-3=0.
設M(x1,y1),N(x2,y2),則有y1+y2=-![]() ,y1y2=-
,y1y2=-![]() .
.
則|y1-y2|=![]() =
=![]() =
=![]() =
=![]() =
=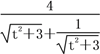 .令
.令![]() =m(m≥
=m(m≥![]() ).易知函數y=m+
).易知函數y=m+![]() 在[
在[![]() ,+∞)上單調遞增,
,+∞)上單調遞增,
則![]() +
+![]() ≥
≥![]() +
+![]() =
=![]() ,當且僅當m=
,當且僅當m=![]() ,即t=0時,取等號.
,即t=0時,取等號.
所以|y1-y2|≤![]() .所以△AMN的面積S=
.所以△AMN的面積S=![]() |AP||y1-y2|≤
|AP||y1-y2|≤![]() ×3×
×3×![]() =
=![]() ,
,
所以Smax=![]() ,此時直線l的方程為x=1.
,此時直線l的方程為x=1.


科目:高中數學 來源: 題型:
【題目】某市縣鄉(xiāng)教師流失現(xiàn)象非常嚴重,為了縣鄉(xiāng)孩子們能接受良好教育,某市今年要為兩所縣鄉(xiāng)中學招聘儲備未來三年的教師,現(xiàn)在每招聘一名教師需要1萬元,若三年后教師嚴重短缺時再招聘,由于各種因素,則每招聘一名教師需要3萬元,已知現(xiàn)在該市縣鄉(xiāng)中學無多余教師,為決策應招聘多少縣鄉(xiāng)教師搜集并整理了該市50所縣鄉(xiāng)中學在過去三年內的教師流失數,得到如表的頻率分布表:
流失教師數 | 6 | 7 | 8 | 9 |
頻數 | 10 | 15 | 15 | 10 |
以這50所縣鄉(xiāng)中學流失教師數的頻率代替一所縣鄉(xiāng)中學流失教師數發(fā)生的概率,記![]() 表示兩所縣鄉(xiāng)中學在過去三年共流失的教師數,
表示兩所縣鄉(xiāng)中學在過去三年共流失的教師數, ![]() 表示今年為兩所縣鄉(xiāng)中學招聘的教師數.為保障縣鄉(xiāng)孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘.
表示今年為兩所縣鄉(xiāng)中學招聘的教師數.為保障縣鄉(xiāng)孩子教育不受影響,若未來三年內教師有短缺,則第四年馬上招聘.
(1)求![]() 的分布列;
的分布列;
(2)若要求![]() ,確定
,確定![]() 的最小值;
的最小值;
(3)以未來四年內招聘教師所需費用的期望值為決策依據,在![]() 與
與![]() 之中選其一,應選用哪個?
之中選其一,應選用哪個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018江蘇南京師大附中、天一、海門、淮陰四校高三聯(lián)考】如圖,一只螞蟻從單位正方體![]() 的頂點
的頂點![]() 出發(fā),每一步(均為等可能性的)經過一條邊到達另一頂點,設該螞蟻經過
出發(fā),每一步(均為等可能性的)經過一條邊到達另一頂點,設該螞蟻經過![]() 步回到點
步回到點![]() 的概率
的概率![]() .
.

(I)分別寫出![]() 的值;
的值;
(II)設頂點![]() 出發(fā)經過
出發(fā)經過![]() 步到達點
步到達點![]() 的概率為
的概率為![]() ,求
,求![]() 的值;
的值;
(III)求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年10月9日,教育部考試中心下發(fā)了《關于2017年普通高考考試大綱修訂內容的通知》,在各科修訂內容中明確提出,增加中華優(yōu)秀傳統(tǒng)文化的考核內容,積極培育和踐行社會主義核心價值觀,充分發(fā)揮高考命題的育人功能和積極導向作用.宿州市教育部門積極回應,編輯傳統(tǒng)文化教材,在全市范圍內開設書法課,經典誦讀等課程.為了了解市民對開設傳統(tǒng)文化課的態(tài)度,教育機構隨機抽取了200位市民進行了解,發(fā)現(xiàn)支持開展的占![]() ,在抽取的男性市民120人中持支持態(tài)度的為80人.
,在抽取的男性市民120人中持支持態(tài)度的為80人.
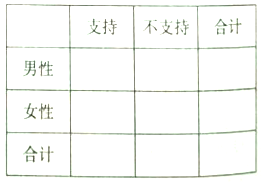
(Ⅰ)完成![]() 列聯(lián)表,并判斷是否有
列聯(lián)表,并判斷是否有![]() 的把握認為性別與支持與否有關?
的把握認為性別與支持與否有關?
(Ⅱ)為了進一步征求對開展傳統(tǒng)文化的意見和建議,從抽取的200位市民中對不支持的按照分層抽樣的方法抽取5位市民,并從抽取的5人中再隨機選取2人進行座談,求選取的2人恰好為1男1女的概率.
附: 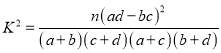 .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著共享單車的成功運營,更多的共享產品逐步走入大家的世界,共享汽車、共享籃球、共享充電寶等各種共享產品層出不窮.某公司隨即抽取![]() 人對共享產品是否對日常生活有益進行了問卷調查,并對參與調查的
人對共享產品是否對日常生活有益進行了問卷調查,并對參與調查的![]() 人中的性別以及意見進行了分類,得到的數據如下表所示:
人中的性別以及意見進行了分類,得到的數據如下表所示:
男 | 女 | 總計 | |
認為共享產品對生活有益 |
|
|
|
認為共享產品對生活無益 |
|
|
|
總計 |
|
|
|
(1)根據表中的數據,能否在犯錯誤的概率不超過![]() 的前提下,認為對共享產品的態(tài)度與性別有關系?
的前提下,認為對共享產品的態(tài)度與性別有關系?
(2)現(xiàn)按照分層抽樣從認為共享產品增多對生活無益的人員中隨機抽取![]() 人,再從
人,再從![]() 人中隨機抽取
人中隨機抽取![]() 人贈送超市購物券作為答謝,求恰有
人贈送超市購物券作為答謝,求恰有![]() 人是女性的概率.
人是女性的概率.
參與公式: 
臨界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱![]() 中,底面
中,底面![]() 為等腰梯形,
為等腰梯形,![]() .
.

(1)證明:![]() ;
;
(2)設![]() 是線段
是線段![]() 上的動點,是否存在這樣的點
上的動點,是否存在這樣的點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ,如果存在,求出
,如果存在,求出![]() 的長;如果不存在,請說明理由.
的長;如果不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com