
【題目】若函數f(x)=x2﹣ex﹣ax在R上存在單調遞增區間,則實數a的取值范圍是 .
【答案】(﹣∞,2ln2﹣2)
【解析】解:∵函數f(x)=x2﹣ex﹣ax,
∴f′(x)=2x﹣ex﹣a,
∵函數f(x)=x2﹣ex﹣ax在R上存在單調遞增區間,
∴f′(x)=2x﹣ex﹣a>0,
即a<2x﹣ex有解,
令g′(x)=2﹣ex ,
g′(x)=2﹣ex=0,x=ln2,
g′(x)=2﹣ex>0,x<ln2,
g′(x)=2﹣ex<0,x>ln2
∴當x=ln2時,g(x)max=2ln2﹣2,
∴a<2ln2﹣2即可.
所以答案是:(﹣∞,2ln2﹣2)
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減).
在這個區間單調遞減).


 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED為矩形,平面BFED⊥平面ABCD,BF=1.
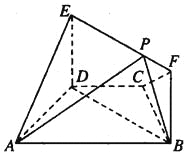
(1)求證:AD⊥平面BFED;
(2)已知點P在線段EF上,![]() =2.求三棱錐E-APD的體積.
=2.求三棱錐E-APD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知曲線C1:y=![]() (x>0)及曲線C2:y=
(x>0)及曲線C2:y=![]() (x>0).C1上的點Pn的橫坐標為an,
(x>0).C1上的點Pn的橫坐標為an,![]() 過C1上的點Pn(n∈N+)作直線平行于x軸,交曲線C2于點Qn,再過點Qn作直線平行于y軸,交曲線C1于點Pn+1.
過C1上的點Pn(n∈N+)作直線平行于x軸,交曲線C2于點Qn,再過點Qn作直線平行于y軸,交曲線C1于點Pn+1.
試求an+1與an之間的關系,并證明a2n-1<![]() <a2n(n∈N+).
<a2n(n∈N+).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1的參數方程為 ![]() (其中θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρcosθ﹣ρsinθ+1=0.
(其中θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρcosθ﹣ρsinθ+1=0.
(1)分別寫出曲線C1與曲線C2的普通方程;
(2)若曲線C1與曲線C2交于A,B兩點,求線段AB的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年,首都北京經歷了59年來霧霾天氣最多的一個月.經氣象局統計,北京市從1月1日至1月30日的30天里有26天出現霧霾天氣,《環境空氣質量指數(AQI)技術規定(試行)》將空氣質量指數分為六級,其中,中度污染(四級)指數為151~200;重度污染(五級)指數為201~300;嚴重污染(六級)指數大于300.下面表1是某觀測點記錄的4天里AQI指數M與當天的空氣水平可見度y(千米)的情況,表2是某氣象觀測點記錄的北京1月1日到1月30日AQI指數頻數的統計結果.
表1
AQI指數M | 900 | 700 | 300 | 100 |
空氣可見度y/千米 | 0.5 | 3.5 | 6.5 | 9.5 |
表2
AQI指數 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
頻數 | 3 | 6 | 12 | 6 | 3 |
(1)設變量x=![]() ,根據表1的數據,求出y關于x的線性回歸方程;
,根據表1的數據,求出y關于x的線性回歸方程;
(2)根據表2估計這30天AQI指數的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Q2=![]() 稱為x,y的二維平方平均數,A2=
稱為x,y的二維平方平均數,A2=![]() 稱為x,y的二維算術平均數,G2=
稱為x,y的二維算術平均數,G2=![]() 稱為x,y的二維幾何平均數,H2=
稱為x,y的二維幾何平均數,H2=![]() 稱為x,y的二維調和平均數,其中x,y均為正數.
稱為x,y的二維調和平均數,其中x,y均為正數.
(1)試判斷G2與H2的大小,并證明你的猜想.
(2)令M=A2﹣G2,N=G2﹣H2,試判斷M與N的大小,并證明你的猜想.
(3)令M=A2﹣G2,N=G2﹣H2,P=Q2﹣A2,試判斷M、N、P三者之間的大小關系,并證明你的猜想.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com