【題目】已知函數f（x）＝|2x﹣1|﹣3|x+1|，設f（x）的最大值為M.
（1）求M；
（2）若正數a，b滿足
Mab，證明：a4b+ab4
.
【答案】（1）M＝3（2）證明見解析；
【解析】
（1）由f（x）＝|2x﹣1|﹣3|x+1|＝|2x﹣1|﹣|2x+2|﹣|x+1|，結合絕對值不等式的性質和絕對值的幾何意義，可得所求最大值；
（2）由（1）可得
3ab，a4b+ab4＝ab（a3+b3）
（
）（a3+b3），再由基本不等式即可得證.
解：（1）函數f（x）＝|2x﹣1|﹣3|x+1|
＝|2x﹣1|﹣|2x+2|﹣|x+1|≤|2x﹣1﹣2x﹣2|﹣|﹣1+1|＝3，
當x＝﹣1時，f（x）取得最大值3，即M＝3；
（2）證明：正數a，b滿足3ab，
故a4b+ab4＝ab（a3+b3）（）（a3+b3）（1+1
）
（2+2
）
，當且僅當a＝b
時等號成立，
故a4b+ab4
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】今年情況特殊，小王在居家自我隔離時對周邊的水產養殖產業進行了研究．
、
兩個投資項目的利潤率分別為投資變量
和
．根據市場分析，和的分布列分別為：
| 5% | 10% | ||
| 0.8 | 0.2 | ||
| 2% | 8% | 12% | |
| 0.2 | 0.5 | 0.3 | |
（1）若在
兩個項目上各投資
萬元，
和
分別表示投資項目和所獲得的利潤，求方差
，
；
（2）若在兩個項目上共投資
萬元，那么如何分配，能使投資項目所得利潤的方差與投資項目所得利潤的方差的和最小，最小值是多少？
（注：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某項數學競賽考試共四道題，考察內容分別為代數、幾何、數論、組合，已知前兩題每題滿分40分，后兩題每題滿分60分，題目難度隨題號依次遞增，已知學生甲答題時，若該題會做則必得滿分，若該題不會做則不作答得0分，通過對學生甲以往測試情況的統計，得到他在同類模擬考試中各題的得分率，如表所示：
假設學生甲每次考試各題的得分相互獨立.
（1）若此項競賽考試四道題的順序依次為代數、幾何、數論、組合，試預測學生甲考試得160分的概率；
（2）學生甲研究該項競賽近五年的試題發現第1題都是代數題，于是他在賽前針對代數版塊進行了強化訓練，并取得了很大進步，現在，只要代數題是在試卷第1、2題的位置，他就一定能答對，若今年該項數學競賽考試四道題的順序依次為代數、數論、組合、幾何，試求學生甲此次考試得分X的分布列.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】請從下面三個條件中任選一個，補充在下面的橫線上，并解答．
①
②
③
的面積為
在中，內角A，B，C所對的邊分別為a，b，c，已知b－c=2，cosA=
， ．
（1）求a；
（2）求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在
中，
，
，
，
分別為
，
的中點
是由
繞直線
旋轉得到，連結
，
，
.
（1）證明：
平面
；
（2）若
，棱
上是否存在一點
，使得
？若存在，確定點 的位置；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對任意
，給定區間
，設函數
表示實數
與所屬的給定區間內唯一整數之差的絕對值.
（1）當
時，求出的解析式；
時，寫出絕對值符號表示的解析式；
（2）求
，
，判斷函數
的奇偶性，并證明你的結論；
（3）當
時，求方程
的實根.（要求說明理由，
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
指數是用體重公斤數除以身高米數的平方得出的數字，是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準．對于高中男體育特長生而言，當數值大于或等于20.5時，我們說體重較重，當數值小于20.5時，我們說體重較輕，身高大于或等于
我們說身高較高，身高小于170cm我們說身高較矮．
（Ⅰ）已知某高中共有32名男體育特長生，其身高與
指數的數據如散點圖，請根據所得信息，完成下述列聯表，并判斷是否有
的把握認為男生的身高對指數有影響．
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
（Ⅱ）①從上述32名男體育特長生中隨機選取8名，其身高和體重的數據如表所示：
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為
．利用已經求得的線性回歸方程，請完善下列殘差表，并求
（解釋變量（身高）對于預報變量（體重）變化的貢獻值）（保留兩位有效數字）；
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重（kg） | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 |
|
|
|
|
|
|
|
②通過殘差分析，對于殘差的最大（絕對值）的那組數據，需要確認在樣本點的采集中是否有人為的錯誤，已知通過重新采集發現，該組數據的體重應該為
．小明重新根據最小二乘法的思想與公式，已算出
，請在小明所算的基礎上求出男體育特長生的身高與體重的線性回歸方程．
參考數據：
，
，
，
，
參考公式：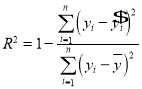
，
，
，
，
．
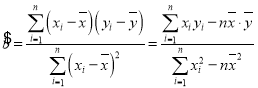| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
