【題目】選修4－1：幾何證明選講
如圖所示，已知PA與⊙O相切，A為切點，PBC為割線，弦CD∥AP，AD、BC相交于E點，F(xiàn)為CE上一點，且DE2=EF·EC
（1）求證：P=EDF；
（2）求證：CE·EB=EF·EP．
【答案】證明見解析．
【解析】（1）要證明兩角P，EDF相等，注意到
，
，因此只要證C，EDF相等，這兩個角正好是可證相似的兩個三角形的對應角，這個相似由已知DE2=EF·EC可證；（2）要證明線段乘積相等，在已知圓中由相交弦定理有CE·EB=ED·EA，再看ED·EA與EF·EP的相等可由相似三角形得到．
試題分析：
試題解析：證明（1）∵DE2=EF·EC，
∴DE CE=EF ED．
∵DEF是公共角，
∴ΔDEF∽ΔCED． ∴EDF=C．
∵CD∥AP， ∴C= P．
∴P=EDF．----5分
（2）∵P=EDF， DEF=PEA，
∴ΔDEF∽ΔPEA．∴DE PE=EF EA．即EF·EP=DE·EA．
∵弦AD、BC相交于點E，∴DE·EA=CE·EB．∴CE·EB=EF·EP． 10分
中考利劍中考試卷匯編系列答案
教育世家狀元卷系列答案
黃岡課堂作業(yè)本系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知在三棱錐
中，
分別是
的中點，
都是正三角形，
.
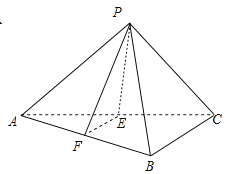
（1）求證：
平面
；
（2）求二面角
的平面角的余弦值；
（3）若點
在一個表面積為
的球面上，求
的邊長.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】給出如下命題:
①命題 “在
中，若
，則
” 的逆命題為真命題;
②若動點
到兩定點
的距離之和為
，則動點的軌跡為線段
;
③若
為假命題，則
都是假命題;
④設(shè)
，則“
”是“
”的必要不充分條件
⑤若實數(shù)
成等比數(shù)列，則圓錐曲線
的離心率為
;
其中所有正確命題的序號是_________.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)f（x）的圖象與函數(shù)h（x）=x+
+2的圖象關(guān)于點A（0,1）對稱.
（1）求f（x）的解析式;
（2）若g（x）=x2·[f（x）-a],且g（x）在區(qū)間[1,2]上為增函數(shù),求實數(shù)a的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】中國天氣網(wǎng)2016年3月4日晚六時通過手機發(fā)布的3月5日通州區(qū)天氣預報的折線圖（如圖），其中上面的折線代表可能出現(xiàn)的從高氣溫，下面的折線代表可能出現(xiàn)的最低氣溫．
（Ⅰ）指出最高氣溫與最低氣溫的相關(guān)性；
（Ⅱ）估計在10:00時最高氣溫和最低氣溫的差；
（Ⅲ）比較最低氣溫與最高氣溫方差的大小（結(jié)論不要求證明）．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
。
（1）當
時，求函數(shù)
在點
處的切線方程；
（2）若函數(shù)
，討論函數(shù)
的單調(diào)性；
（3）若（2）中函數(shù)有兩個極值點
，且不等式
恒成立，求實數(shù)
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
的左、右焦點分別為
，
直線
與橢圓
的一個交點為
，點
是橢圓上的任意—點，延長
交橢圓于點
，連接
.
（1）求橢圓
的方程；
（2）求
的內(nèi)切圓的最大周長.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】“健步走”是一種方便而又有效的鍛煉方式，李老師每天堅持“健步走”，并用計步器進行統(tǒng)計．他最近8天“健步走”步數(shù)的條形統(tǒng)計圖及相應的消耗能量數(shù)據(jù)表如下：
（1）求李老師這8天“健步走”步數(shù)的平均數(shù)；
（2）從步數(shù)為16千步，17千步，18千步的6天中任選2天，設(shè)李老師這2天通過“健步走”消耗的能量和為
，求
的分布列及數(shù)學期望．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com