
【題目】已知函數![]() .
.
(Ⅰ)![]() 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(Ⅱ)已知a,b,c是△ABC三邊長,且f(C)=2,△ABC的面積S=![]() ,c=7.求角C及a,b的值.
,c=7.求角C及a,b的值.
【答案】(1)π, 函數f(x)的遞增區間是[﹣![]() +kπ,
+kπ, ![]() +kπ],k∈Z;(2) a=8,b=5或a=5,b=8.
+kπ],k∈Z;(2) a=8,b=5或a=5,b=8.
【解析】試題分析: ![]() 解析式利用兩角和與差的正弦函數公式及二倍角的余弦函數公式化簡,整理為一個角的正弦函數,找出
解析式利用兩角和與差的正弦函數公式及二倍角的余弦函數公式化簡,整理為一個角的正弦函數,找出![]() 的值代入周期公式即可求出
的值代入周期公式即可求出![]() 的最小正周期,利用正弦函數的單調性即可求出
的最小正周期,利用正弦函數的單調性即可求出![]() 的單調遞增區間。
的單調遞增區間。
![]() 由
由![]() ,根據第一問確定出的解析式求出
,根據第一問確定出的解析式求出![]() 的度數,利用三角形面積公式列出關系式,將
的度數,利用三角形面積公式列出關系式,將![]() 值代入求出
值代入求出![]() 的值,利用余弦定理列出關系式,將
的值,利用余弦定理列出關系式,將![]() 代入求出
代入求出![]() 的值,聯立即可求出
的值,聯立即可求出![]() 的值。
的值。
解析:(Ⅰ)f(x)=sin2xcos![]() +cos2xsin
+cos2xsin![]() +sin2xcos
+sin2xcos![]() ﹣cos2xsin
﹣cos2xsin![]() +cos2x+1=
+cos2x+1=![]() sin2x+cos2x+1=2sin(2x+
sin2x+cos2x+1=2sin(2x+![]() )+1,
)+1,
∵ω=2,∴T=![]() =π;
=π;
令﹣![]() +2kπ≤2x+
+2kπ≤2x+![]() ≤
≤![]() +2kπ,k∈Z,得到﹣
+2kπ,k∈Z,得到﹣![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z,
+kπ,k∈Z,
則函數f(x)的遞增區間是[﹣![]() +kπ,
+kπ,![]() +kπ],k∈Z;
+kπ],k∈Z;
(Ⅱ)由f(C)=2,得到2sin(2C+![]() )+1=2,即sin(2C+
)+1=2,即sin(2C+![]() )=
)=![]() ,
,
∴2C+![]() =
=![]() 或2C+
或2C+![]() =
=![]() ,
,
解得:C=0(舍去)或C=![]() ,
,
∵S=10![]() ,
,
∴![]() absinC=
absinC=![]() ab=10
ab=10![]() ,即ab=40①,
,即ab=40①,
由余弦定理得:c2=a2+b2﹣2abcosC,即49=a2+b2﹣ab,
將ab=40代入得:a2+b2=89②,
聯立①②解得:a=8,b=5或a=5,b=8.


科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域均為
的定義域均為![]() ,且
,且![]() 是奇函數,
是奇函數,![]() 是偶函數,
是偶函數,![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)求![]() 的解析式,并證明:當
的解析式,并證明:當![]() 時,
時,![]() ;
;
(2)若關于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+)(ω>0,0≤≤π)為偶函數,其圖象上相鄰的兩個最高點之間的距離為2π.
(1)求f(x)的解析式;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有甲、乙兩個班級進行數學考試,按照大于等于85分為優秀,85分以下為非優秀統計成績后,得到如下的列聯表.
已知從全部105人中隨機抽取1人為優秀的概率為![]() .
.
(1)請完成上面的列聯表:若按![]() 的可靠性要求,根據列聯表的數據,能否認為“成績與班級有關系”;
的可靠性要求,根據列聯表的數據,能否認為“成績與班級有關系”;
(2)若按下面的方法從甲班優秀的學生中抽取一人:把甲班優秀的10名學生從2到11進行編號,先后兩次拋擲一枚均勻的骰子,出現的點數之和為被抽取人的序號.試求抽到10號的概率.

附: 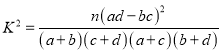

查看答案和解析>>
科目:高中數學 來源: 題型:
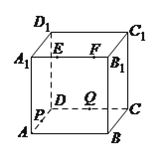
【題目】如圖,正方體![]() 的棱長為
的棱長為![]() ,動點
,動點![]() 、
、![]() 在棱
在棱![]() 上,動點
上,動點![]() ,
,![]() 分別在棱
分別在棱![]() ,
,![]() 上,若
上,若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() ,
,![]() 大于零),則四面體
大于零),則四面體![]() 的體積( ).
的體積( ).
A. 與![]() ,
,![]() ,
,![]() 都有關 B. 與
都有關 B. 與![]() 有關,與
有關,與![]() ,
,![]() 無關
無關
C. 與![]() 有關,與
有關,與![]() ,
,![]() 無關 D. 與
無關 D. 與![]() 有關,與
有關,與![]() ,
,![]() 無關
無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠有4臺大型機器,在一個月中,一臺機器至多出現1次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需1名工人進行維修,每臺機器出現故障需要維修的概率為![]() .
.
(1)若出現故障的機器臺數為![]() ,求
,求![]() 的分布列;
的分布列;
(2) 該廠至少有多少名工人才能保證每臺機器在任何時刻同時出現故障時能及時進行維修的概率不少于90%?
(3)已知一名工人每月只有維修1臺機器的能力,每月需支付給每位工人1萬元的工資,每臺機器不出現故障或出現故障能及時維修,就使該廠產生5萬元的利潤,否則將不產生利潤,若該廠現有2名工人,求該廠每月獲利的均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正方體![]() 的棱長為1,
的棱長為1, ![]() 分別是棱
分別是棱![]() 的中點,過直線
的中點,過直線![]() 的平面分別與棱
的平面分別與棱![]() 交于
交于![]() ,設
,設![]() ,
, ![]() ,給出以下四個命題:
,給出以下四個命題:
①![]()
②當且僅當![]() 時,四邊形
時,四邊形![]() 的面積最小;
的面積最小;
③四邊形![]() 周長
周長![]() ,
, ![]() ,則
,則![]() 是奇函數;
是奇函數;
④四棱錐![]() 的體積
的體積![]() 為常函數;
為常函數;
其中正確命題的個數為( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com