
【題目】為研究冬季晝夜溫差大小對(duì)某反季節(jié)大豆新品種發(fā)芽率的影響,某校課外興趣小組記錄了![]() 組晝夜溫差與
組晝夜溫差與![]() 顆種子發(fā)芽數(shù),得到如下資料:
顆種子發(fā)芽數(shù),得到如下資料:
組號(hào) | 1 | 2 | 3 | 4 | 5 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發(fā)芽數(shù) | 23 | 25 | 30 | 26 | 16 |
經(jīng)分析,這組數(shù)據(jù)具有較強(qiáng)的線性相關(guān)關(guān)系,因此該小組確定的研究方案是:先從這五組數(shù)據(jù)中選取![]() 組數(shù)據(jù)求出線性回歸方程,再用沒選取的
組數(shù)據(jù)求出線性回歸方程,再用沒選取的![]() 組數(shù)據(jù)進(jìn)行檢驗(yàn).
組數(shù)據(jù)進(jìn)行檢驗(yàn).
(1)若選取的是第![]() 組的數(shù)據(jù),求出
組的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由線性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過![]() 顆,則認(rèn)為得到的線性回歸方程是可靠的,試問(1)中所得的線性回歸方程是否可靠?
顆,則認(rèn)為得到的線性回歸方程是可靠的,試問(1)中所得的線性回歸方程是否可靠?
(參考公式: ,
,![]() )
)
【答案】(1)![]() (2)可靠
(2)可靠
【解析】
(1)根據(jù)所給的數(shù)據(jù),先做出![]() 的平均數(shù),即做出本組數(shù)據(jù)的樣本中心點(diǎn),根據(jù)最小二乘法求出線性回歸方程的系數(shù),寫出線性回歸方程;(2)根據(jù)估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過2顆,就認(rèn)為得到的線性回歸方程是可靠的,根據(jù)求得的結(jié)果和所給的數(shù)據(jù)進(jìn)行比較,得到所求的方程是可靠的.
的平均數(shù),即做出本組數(shù)據(jù)的樣本中心點(diǎn),根據(jù)最小二乘法求出線性回歸方程的系數(shù),寫出線性回歸方程;(2)根據(jù)估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過2顆,就認(rèn)為得到的線性回歸方程是可靠的,根據(jù)求得的結(jié)果和所給的數(shù)據(jù)進(jìn)行比較,得到所求的方程是可靠的.
(1)由題意:![]() ,
,![]() ,
,

![]() .
.
![]() ,
,
故回歸直線方程為:![]() .
.
(2)當(dāng)![]() 時(shí),
時(shí),![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,所以(1)中所得的回歸直線方程是可靠的.
,所以(1)中所得的回歸直線方程是可靠的.


 南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
南大教輔搶先起跑暑假銜接教程南京大學(xué)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于區(qū)間[a,b](a<b),若函數(shù)![]() 同時(shí)滿足:①
同時(shí)滿足:①![]() 在[a,b]上是單調(diào)函數(shù),②函數(shù)
在[a,b]上是單調(diào)函數(shù),②函數(shù)![]() 在[a,b]的值域是[a,b],則稱區(qū)間[a,b]為函數(shù)
在[a,b]的值域是[a,b],則稱區(qū)間[a,b]為函數(shù)![]() 的“保值”區(qū)間
的“保值”區(qū)間
(1)求函數(shù)![]() 的所有“保值”區(qū)間
的所有“保值”區(qū)間
(2)函數(shù)![]() 是否存在“保值”區(qū)間?若存在,求
是否存在“保值”區(qū)間?若存在,求![]() 的取值范圍,若不存在,說明理由
的取值范圍,若不存在,說明理由
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是 ( )
A. “若![]() ,則
,則![]() ,或
,或![]() ”的否定是“若
”的否定是“若![]() 則
則![]() ,或
,或 ![]() ”
”
B. a,b是兩個(gè)命題,如果a是b的充分條件,那么![]() 是
是![]() 的必要條件.
的必要條件.
C. 命題“![]() ,使 得
,使 得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有 ![]() ”
”
D. 命題“ 若![]() ,則
,則![]() ”的否命題為真命題.
”的否命題為真命題.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定圓![]() ,動(dòng)圓
,動(dòng)圓![]() 過點(diǎn)
過點(diǎn)![]() 且與圓
且與圓![]() 相切,記圓心
相切,記圓心![]() 的軌跡為
的軌跡為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 在
在![]() 上運(yùn)動(dòng),
上運(yùn)動(dòng),![]() 與
與![]() 關(guān)于原點(diǎn)對(duì)稱,且
關(guān)于原點(diǎn)對(duì)稱,且![]() ,當(dāng)
,當(dāng)![]() 的面積最小時(shí), 求直線
的面積最小時(shí), 求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】青少年“心理健康”問題越來越引起社會(huì)關(guān)注,某校對(duì)高一600名學(xué)生進(jìn)行了一次“心理健康”知識(shí)測(cè)試,并從中抽取了部分學(xué)生的成績(jī)(得分取正整數(shù),滿分100分)作為樣本,繪制了下面尚未完成的頻率分布表和頻率分布直方圖。
分組 | 頻數(shù) | 頻率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合計(jì) | 1.00 |
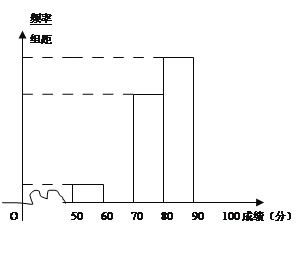
(1)填寫答題卡頻率分布表中的空格,補(bǔ)全頻率分布直方圖,并標(biāo)出每個(gè)小矩形對(duì)應(yīng)的縱軸數(shù)據(jù);
(2)請(qǐng)你估算學(xué)生成績(jī)的平均數(shù)及中位數(shù)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)對(duì)任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0時(shí),恒有f(x)<1.
(1)試判斷f(x)在R上的單調(diào)性,并加以證明;
(2)若f(3)=4,解不等式f(a2+a-5)<2
(3)若關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求實(shí)數(shù)
上有解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() ,點(diǎn)
,點(diǎn)![]() ,直線
,直線![]() .
.
(1)求與圓![]() 相切,且與直線
相切,且與直線![]() 垂直的直線方程;
垂直的直線方程;
(2)在直線![]() 上(
上(![]() 為坐標(biāo)原點(diǎn)),存在定點(diǎn)
為坐標(biāo)原點(diǎn)),存在定點(diǎn)![]() (不同于點(diǎn)
(不同于點(diǎn)![]() ),滿足:對(duì)于圓
),滿足:對(duì)于圓![]() 上任一點(diǎn)
上任一點(diǎn)![]() ,都有
,都有![]() 為一常數(shù),試求所有滿足條件的點(diǎn)
為一常數(shù),試求所有滿足條件的點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
【答案】(1)![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析:
(1)設(shè)所求直線方程為![]() ,利用圓心到直線的距離等于半徑可得關(guān)于b的方程,解方程可得
,利用圓心到直線的距離等于半徑可得關(guān)于b的方程,解方程可得![]() ,則所求直線方程為
,則所求直線方程為![]()
(2)方法1:假設(shè)存在這樣的點(diǎn)![]() ,由題意可得
,由題意可得![]() ,則
,則![]() ,然后證明
,然后證明![]() 為常數(shù)
為常數(shù)![]() 為即可.
為即可.
方法2:假設(shè)存在這樣的點(diǎn)![]() ,使得
,使得![]() 為常數(shù)
為常數(shù)![]() ,則
,則![]() ,據(jù)此得到關(guān)于
,據(jù)此得到關(guān)于![]() 的方程組,求解方程組可得存在點(diǎn)
的方程組,求解方程組可得存在點(diǎn)![]() 對(duì)于圓
對(duì)于圓![]() 上任一點(diǎn)
上任一點(diǎn)![]() ,都有
,都有![]() 為常數(shù)
為常數(shù)![]() .
.
試題解析:
(1)設(shè)所求直線方程為![]() ,即
,即![]() ,
,
∵直線與圓相切,∴![]() ,得
,得![]() ,
,
∴所求直線方程為![]()
(2)方法1:假設(shè)存在這樣的點(diǎn)![]() ,
,
當(dāng)![]() 為圓
為圓![]() 與
與![]() 軸左交點(diǎn)
軸左交點(diǎn)![]() 時(shí),
時(shí),![]() ;
;
當(dāng)![]() 為圓
為圓![]() 與
與![]() 軸右交點(diǎn)
軸右交點(diǎn)![]() 時(shí),
時(shí),![]() ,
,
依題意,![]() ,解得,
,解得,![]() (舍去),或
(舍去),或![]() .
.
下面證明點(diǎn)![]() 對(duì)于圓
對(duì)于圓![]() 上任一點(diǎn)
上任一點(diǎn)![]() ,都有
,都有![]() 為一常數(shù).
為一常數(shù).
設(shè)![]() ,則
,則![]() ,
,
∴![]()
![]()
![]() ,
,
從而![]() 為常數(shù).
為常數(shù).
方法2:假設(shè)存在這樣的點(diǎn)![]() ,使得
,使得![]() 為常數(shù)
為常數(shù)![]() ,則
,則![]() ,
,
∴![]() ,將
,將![]() 代入得,
代入得,
![]() ,即
,即
![]() 對(duì)
對(duì)![]() 恒成立,
恒成立,
∴![]() ,解得
,解得 或
或![]() (舍去),
(舍去),
所以存在點(diǎn)![]() 對(duì)于圓
對(duì)于圓![]() 上任一點(diǎn)
上任一點(diǎn)![]() ,都有
,都有![]() 為常數(shù)
為常數(shù)![]() .
.
點(diǎn)睛:求定值問題常見的方法有兩種:
(1)從特殊入手,求出定值,再證明這個(gè)值與變量無關(guān).
(2)直接推理、計(jì)算,并在計(jì)算推理的過程中消去變量,從而得到定值.
【題型】解答題
【結(jié)束】
22
【題目】已知函數(shù)![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,其中
,其中![]() 為常數(shù).
為常數(shù).
(1)當(dāng)![]() 時(shí),求
時(shí),求![]() 的最大值,并推斷方程
的最大值,并推斷方程![]() 是否有實(shí)數(shù)解;
是否有實(shí)數(shù)解;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上的最大值為-3,求
上的最大值為-3,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,直線
,直線![]() ,設(shè)圓
,設(shè)圓![]() 的半徑為1, 圓心在
的半徑為1, 圓心在![]() 上.
上.

(1)若圓心![]() 也在直線
也在直線![]() 上,過點(diǎn)
上,過點(diǎn)![]() 作圓
作圓![]() 的切線,求切線方程;
的切線,求切線方程;
(2)若圓![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使
,使![]() ,求圓心
,求圓心![]() 的橫坐標(biāo)
的橫坐標(biāo)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若![]() 為定義域
為定義域![]() 上的單調(diào)函數(shù),且存在區(qū)間
上的單調(diào)函數(shù),且存在區(qū)間![]() (其中
(其中![]() ,使得當(dāng)
,使得當(dāng)![]() 時(shí),
時(shí), ![]() 的取值范圍恰為
的取值范圍恰為![]() ,則稱函數(shù)
,則稱函數(shù)![]() 是
是![]() 上的“優(yōu)美函數(shù)”.
上的“優(yōu)美函數(shù)”.
![]() 函數(shù)
函數(shù)![]() 是否為“優(yōu)美函數(shù)”?若是,求出
是否為“優(yōu)美函數(shù)”?若是,求出![]() 的值;若不是,請(qǐng)說明理由.
的值;若不是,請(qǐng)說明理由.
![]() 若
若![]() 為“優(yōu)美函數(shù)”,求實(shí)數(shù)
為“優(yōu)美函數(shù)”,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
![]() 若函數(shù)
若函數(shù)![]() 為“優(yōu)美函數(shù)”,求實(shí)數(shù)
為“優(yōu)美函數(shù)”,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com