
【題目】在直角坐標系xOy中,曲線C:![]() 與直線l:
與直線l:![]() 交于M,N兩點.
交于M,N兩點.
![]() 當
當![]() 時,求
時,求![]() 的面積的取值范圍;
的面積的取值范圍;
![]() 軸上是否存在點P,使得當k變動時,總有
軸上是否存在點P,使得當k變動時,總有![]() ?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
?若存在,求以線段OP為直徑的圓的方程;若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)聯立直線的方程和拋物線的方程,寫出韋達定理,利用弦長公式求得![]() ,用點到直線的距離公式求得
,用點到直線的距離公式求得![]() 到直線的距離,由此可求得三角形
到直線的距離,由此可求得三角形![]() 面積的表達式.再利用
面積的表達式.再利用![]() 的取值范圍求得面積的取值范圍.(2)設出
的取值范圍求得面積的取值范圍.(2)設出![]() 點的坐標,寫出直線
點的坐標,寫出直線![]() 的斜率,然后相加,利用(1)的韋達定理條件化簡,并令斜率和為零,由此求得
的斜率,然后相加,利用(1)的韋達定理條件化簡,并令斜率和為零,由此求得![]() 點的坐標,進而求得以
點的坐標,進而求得以![]() 為直徑的圓的方程.
為直徑的圓的方程.
(1)將![]() 代入
代入![]() ,得
,得![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
從而![]() .
.
因為![]() 到
到![]() 的距離為
的距離為![]() ,
,
所以![]() 的面積
的面積![]() .
.
因為![]() ,所以
,所以![]() .
.
(2)存在符合題意的點,證明如下:
設![]() 為符合題意的點,直線
為符合題意的點,直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
從而![]()
![]()
![]() .
.
當![]() 時,有
時,有![]() ,則直線
,則直線![]() 的傾斜角與直線
的傾斜角與直線![]() 的傾斜角互補,
的傾斜角互補,
故![]() ,所以點
,所以點![]() 符合題意.
符合題意.
故以線段![]() 為直徑的圓的方程為
為直徑的圓的方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象與直線y=m分別交于AB兩點,則( )
的圖象與直線y=m分別交于AB兩點,則( )
A.f(x)圖像上任一點與曲線g(x)上任一點連線線段的最小值為2+ln2
B.m使得曲線g(x)在B處的切線平行于曲線f(x)在A處的切線
C.函數f(x)-g(x)+m不存在零點
D.m使得曲線g(x)在點B處的切線也是曲線f(x)的切線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學界的震動.在1859年,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,
的結論.若根據歐拉得出的結論,估計10000以內的素數的個數為(素數即質數,![]() ,計算結果取整數)
,計算結果取整數)
A. 1089 B. 1086 C. 434 D. 145
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知斜率為1的直線與拋物線![]() 交于
交于![]() 兩點,
兩點,![]() 中點的橫坐標為2.
中點的橫坐標為2.
(1)求拋物線![]() 的方程;
的方程;
(2)設直線![]() 交
交![]() 軸于點
軸于點![]() ,交拋物線
,交拋物線![]() 于點
于點![]() ,
,![]() 關于點
關于點![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() 并延長交
并延長交![]() 于點
于點![]() .除
.除![]() 以外,直線
以外,直線![]() 與
與![]() 是否有其它公共點?請說明理由.
是否有其它公共點?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐VABCD中,底面ABCD是矩形,VD⊥平面ABCD,過AD的平面分別與VB,VC交于點M,N.

(1) 求證:BC⊥平面VCD;
(2) 求證:AD∥MN.
查看答案和解析>>
科目:高中數學 來源: 題型:
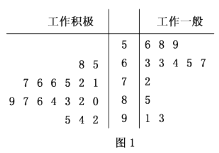
【題目】某大型企業人力資源部為了研究企業員工工作積極性和對待企業改革態度的關系,隨機抽取了![]() 名員工進行問卷調查,其中
名員工進行問卷調查,其中![]() 的員工工作積極.經匯總調查,這
的員工工作積極.經匯總調查,這![]() 名員工是否支持企業改革的調查得分(百分制)如莖葉圖(圖
名員工是否支持企業改革的調查得分(百分制)如莖葉圖(圖![]() )所示.調查評價標準指出:調查得分不低于
)所示.調查評價標準指出:調查得分不低于![]() 分者為積極支持企業改革,調查得分低于70分者不太贊成企業改革.
分者為積極支持企業改革,調查得分低于70分者不太贊成企業改革.
(1)根據以上資料完成下面的![]() 列聯表,結合數據能否有
列聯表,結合數據能否有![]() 的把握認為員工的工作積極性與“是否積極支持企業改革”是有關的,并回答人力資源部的研究項目.
的把握認為員工的工作積極性與“是否積極支持企業改革”是有關的,并回答人力資源部的研究項目.
積極支持企業改革 | 不太贊成企業改革 | 總計 | |
工作積極 | |||
工作一般 | |||
總計 |
(2)現將![]() 名員工的調查得分分為如下
名員工的調查得分分為如下![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
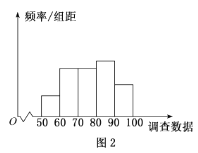
,![]() 其頻率分布直方圖如圖
其頻率分布直方圖如圖![]() 所示,這
所示,這![]() 名員工的調查數據得分的平均值可由莖葉圖得到,記為
名員工的調查數據得分的平均值可由莖葉圖得到,記為![]() ,由頻率分布直方圖得到的估計值記為
,由頻率分布直方圖得到的估計值記為![]() (同一組中的數據用該組區間的中點值作代表),
(同一組中的數據用該組區間的中點值作代表),![]() 與
與![]() 的誤差值在
的誤差值在![]() 以內,可以由
以內,可以由![]() 代替
代替![]() ,能否由
,能否由![]() 代替
代替![]() ?(提示:
?(提示:![]() 名員工的調查數據得分的和
名員工的調查數據得分的和![]() )
)
(3)該企業人力資源部從![]() 分以上的員工中任選
分以上的員工中任選![]() 名員工進行座談,則所選員工的分數超過
名員工進行座談,則所選員工的分數超過![]() 分的人數的數學期望是多少?
分的人數的數學期望是多少?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P—ABC中,PC![]() 底面ABC,AB=BC,D、F分別為AC、PC的中點,DE
底面ABC,AB=BC,D、F分別為AC、PC的中點,DE![]() AP于E。(1)求證:AP
AP于E。(1)求證:AP![]() 平面BDE;(2)求證:平面BDE
平面BDE;(2)求證:平面BDE![]() 平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。
平面BDF;(3)若AE:EP=1:2,求截面BEF分三棱錐P—ABC所成上、下兩部分的體積比。

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》卷第六《均輸》中,提到如下問題:“今有竹九節,下三節容量四升,上四節容量三升.問中間二節欲均容,各多少?”其大致意思是說,若九節竹每節的容量依次成等差數列,下三節容量四升,上四節容量三升,則中間兩節的容量各是( )
A.![]() 升、
升、![]() 升B.
升B.![]() 升、
升、![]() 升
升
C.![]() 升、
升、![]() 升D.
升D.![]() 升、
升、![]() 升
升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四個函數![]() ,其中
,其中![]() ,
,![]() 的圖像如圖所示.
的圖像如圖所示.

(1)請在坐標系中畫出![]() ,
,![]() 的圖像,并根據這四個函數的圖像總結出指數函數具有哪些性質?
的圖像,并根據這四個函數的圖像總結出指數函數具有哪些性質?
(2)舉出在實際情境中能夠抽象出指數函數的一個例子并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com