
【題目】為了提高生產(chǎn)線(xiàn)的運(yùn)行效率,工廠(chǎng)對(duì)生產(chǎn)線(xiàn)的設(shè)備進(jìn)行了技術(shù)改造.為了對(duì)比技術(shù)改造后的效果,采集了生產(chǎn)線(xiàn)的技術(shù)改造前后各20次連續(xù)正常運(yùn)行的時(shí)間長(zhǎng)度(單位:天)數(shù)據(jù),并繪制了如下莖葉圖:
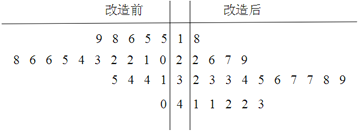
(Ⅰ)(1)設(shè)所采集的40個(gè)連續(xù)正常運(yùn)行時(shí)間的中位數(shù)![]() ,并將連續(xù)正常運(yùn)行時(shí)間超過(guò)
,并將連續(xù)正常運(yùn)行時(shí)間超過(guò)![]() 和不超過(guò)
和不超過(guò)![]() 的次數(shù)填入下面的列聯(lián)表:
的次數(shù)填入下面的列聯(lián)表:
超過(guò) | 不超過(guò) | |
改造前 |
|
|
改造后 |
|
|
試寫(xiě)出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)根據(jù)(1)中的列聯(lián)表,能否有![]() 的把握認(rèn)為生產(chǎn)線(xiàn)技術(shù)改造前后的連續(xù)正常運(yùn)行時(shí)間有差異?
的把握認(rèn)為生產(chǎn)線(xiàn)技術(shù)改造前后的連續(xù)正常運(yùn)行時(shí)間有差異?
附: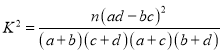 ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(Ⅱ)工廠(chǎng)的生產(chǎn)線(xiàn)的運(yùn)行需要進(jìn)行維護(hù).工廠(chǎng)對(duì)生產(chǎn)線(xiàn)的生產(chǎn)維護(hù)費(fèi)用包括正常維護(hù)費(fèi)、保障維護(hù)費(fèi)兩種對(duì)生產(chǎn)線(xiàn)設(shè)定維護(hù)周期為![]() 天(即從開(kāi)工運(yùn)行到第
天(即從開(kāi)工運(yùn)行到第![]() 天(
天(![]() )進(jìn)行維護(hù).生產(chǎn)線(xiàn)在一個(gè)生產(chǎn)周期內(nèi)設(shè)置幾個(gè)維護(hù)周期,每個(gè)維護(hù)周期相互獨(dú)立.在一個(gè)維護(hù)周期內(nèi),若生產(chǎn)線(xiàn)能連續(xù)運(yùn)行,則不會(huì)產(chǎn)生保障維護(hù)費(fèi);若生產(chǎn)線(xiàn)不能連續(xù)運(yùn)行,則產(chǎn)生保障維護(hù)費(fèi).經(jīng)測(cè)算,正常維護(hù)費(fèi)為0.5萬(wàn)元
)進(jìn)行維護(hù).生產(chǎn)線(xiàn)在一個(gè)生產(chǎn)周期內(nèi)設(shè)置幾個(gè)維護(hù)周期,每個(gè)維護(hù)周期相互獨(dú)立.在一個(gè)維護(hù)周期內(nèi),若生產(chǎn)線(xiàn)能連續(xù)運(yùn)行,則不會(huì)產(chǎn)生保障維護(hù)費(fèi);若生產(chǎn)線(xiàn)不能連續(xù)運(yùn)行,則產(chǎn)生保障維護(hù)費(fèi).經(jīng)測(cè)算,正常維護(hù)費(fèi)為0.5萬(wàn)元![]() 次;保障維護(hù)費(fèi)第一次為0.2萬(wàn)元
次;保障維護(hù)費(fèi)第一次為0.2萬(wàn)元![]() 周期,此后每增加一次則保障維護(hù)費(fèi)增加0.2萬(wàn)元.現(xiàn)制定生產(chǎn)線(xiàn)一個(gè)生產(chǎn)周期(以120天計(jì))內(nèi)的維護(hù)方案:
周期,此后每增加一次則保障維護(hù)費(fèi)增加0.2萬(wàn)元.現(xiàn)制定生產(chǎn)線(xiàn)一個(gè)生產(chǎn)周期(以120天計(jì))內(nèi)的維護(hù)方案:![]() ,
,![]() ,2,3,4.以生產(chǎn)線(xiàn)在技術(shù)改造后一個(gè)維護(hù)周期內(nèi)能連續(xù)正常運(yùn)行的頻率作為概率,求一個(gè)生產(chǎn)周期內(nèi)生產(chǎn)維護(hù)費(fèi)的分布列及期望值.
,2,3,4.以生產(chǎn)線(xiàn)在技術(shù)改造后一個(gè)維護(hù)周期內(nèi)能連續(xù)正常運(yùn)行的頻率作為概率,求一個(gè)生產(chǎn)周期內(nèi)生產(chǎn)維護(hù)費(fèi)的分布列及期望值.
【答案】(Ⅰ)(1)![]() ,
,![]() ,
,![]() ,
,![]() ,(2)有
,(2)有![]() 的把握認(rèn)為連續(xù)正常運(yùn)行時(shí)間有差異;(Ⅱ)分布列見(jiàn)解析,2.275萬(wàn)元.
的把握認(rèn)為連續(xù)正常運(yùn)行時(shí)間有差異;(Ⅱ)分布列見(jiàn)解析,2.275萬(wàn)元.
【解析】
(Ⅰ)根據(jù)莖葉圖得到![]() ,
,![]() ,
,![]() ,
,![]() ,計(jì)算
,計(jì)算![]() ,得到答案.
,得到答案.
(Ⅱ)計(jì)算得到![]() ,得到分布列,計(jì)算數(shù)學(xué)期望得到答案.
,得到分布列,計(jì)算數(shù)學(xué)期望得到答案.
(Ⅰ)(1)由莖葉圖知![]() ,根據(jù)莖葉圖可得:
,根據(jù)莖葉圖可得:![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)由于![]() ,所以有
,所以有![]() 的把握認(rèn)為連續(xù)正常運(yùn)行時(shí)間有差異.
的把握認(rèn)為連續(xù)正常運(yùn)行時(shí)間有差異.
(Ⅱ)生產(chǎn)周期內(nèi)有4個(gè)維護(hù)周期,一個(gè)維護(hù)周期為30天,一個(gè)維護(hù)周期內(nèi),生產(chǎn)線(xiàn)需保障維護(hù)的概率為![]() .
.
設(shè)一個(gè)生產(chǎn)周期內(nèi)需保障維護(hù)的次數(shù)為![]() 次,則正常維護(hù)費(fèi)為
次,則正常維護(hù)費(fèi)為![]() 萬(wàn)元,保障維護(hù)費(fèi)為
萬(wàn)元,保障維護(hù)費(fèi)為![]() 萬(wàn)元.
萬(wàn)元.
故一個(gè)生產(chǎn)周期內(nèi)需保障維護(hù)![]() 次時(shí)的生產(chǎn)維護(hù)費(fèi)為
次時(shí)的生產(chǎn)維護(hù)費(fèi)為![]() 萬(wàn)元.
萬(wàn)元.
由于![]() ,設(shè)一個(gè)生產(chǎn)周期內(nèi)的生產(chǎn)維護(hù)費(fèi)為
,設(shè)一個(gè)生產(chǎn)周期內(nèi)的生產(chǎn)維護(hù)費(fèi)為![]() 萬(wàn)元,則分布列為
萬(wàn)元,則分布列為
| 2 | 2.2 | 2.6 | 3.2 | 4 |
|
|
|
|
|
|
則![]()
![]() 萬(wàn)元.
萬(wàn)元.
故一個(gè)生產(chǎn)周期內(nèi)生產(chǎn)維護(hù)費(fèi)的期望值為2.275萬(wàn)元.


 舉一反三單元同步過(guò)關(guān)卷系列答案
舉一反三單元同步過(guò)關(guān)卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
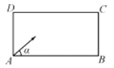
【題目】臺(tái)球運(yùn)動(dòng)已有五、六百年的歷史,參與者用球桿在臺(tái)上擊球.若和光線(xiàn)一樣,臺(tái)球在球臺(tái)上碰到障礙物后也遵從反射定律如圖,有一張長(zhǎng)方形球臺(tái)ABCD,![]() ,現(xiàn)從角落A沿角
,現(xiàn)從角落A沿角![]() 的方向把球打出去,球經(jīng)2次碰撞球臺(tái)內(nèi)沿后進(jìn)入角落C的球袋中,則
的方向把球打出去,球經(jīng)2次碰撞球臺(tái)內(nèi)沿后進(jìn)入角落C的球袋中,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著人們生活水平的不斷提高,肥胖人數(shù)不斷增多.世界衛(wèi)生組織(WHO)常用身體質(zhì)量指數(shù)(BMI)來(lái)衡量人體胖瘦成度以及是否健康,其計(jì)算公式是![]() .成人的BMI數(shù)值標(biāo)準(zhǔn)為:BMI
.成人的BMI數(shù)值標(biāo)準(zhǔn)為:BMI![]() 偏瘦;
偏瘦;![]() BMI
BMI![]() 為正常;
為正常;![]() BMI
BMI![]() 為偏胖;BMI
為偏胖;BMI![]() 為肥胖.某研究機(jī)構(gòu)為了解某快遞公司員工的身體質(zhì)量指數(shù),研究人員從公司員工體檢數(shù)據(jù)中,抽取了8名員工(編號(hào)1-8)的身高
為肥胖.某研究機(jī)構(gòu)為了解某快遞公司員工的身體質(zhì)量指數(shù),研究人員從公司員工體檢數(shù)據(jù)中,抽取了8名員工(編號(hào)1-8)的身高![]() (cm)和體重
(cm)和體重![]() (kg)數(shù)據(jù),并計(jì)算得到他們的BMI(精確到0.1)如下表:
(kg)數(shù)據(jù),并計(jì)算得到他們的BMI(精確到0.1)如下表:
編 號(hào) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高(cm) | 163 | 164 | 165 | 168 | 170 | 172 | 176 | 182 |
體重(kg) | 54 | 60 | 77 | 72 | 68 | ● | 72 | 55 |
BMI(近似值) | 20.3 | 22.3 | 28.3 | 25.5 | 23.5 | 23.7 | 23.2 | 16.6 |
(1)現(xiàn)從這8名員工中選取3人進(jìn)行復(fù)檢,記抽取到BMI值為“正常”員工的人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
(2)研究機(jī)構(gòu)分析發(fā)現(xiàn)公司員工的身高![]() (cm)和體重
(cm)和體重![]() (kg)之間有較強(qiáng)的線(xiàn)性相關(guān)關(guān)系,在編號(hào)為6的體檢數(shù)據(jù)丟失之前調(diào)查員甲已進(jìn)行相關(guān)的數(shù)據(jù)分析,并計(jì)算得出該組數(shù)據(jù)的線(xiàn)性回歸方程為
(kg)之間有較強(qiáng)的線(xiàn)性相關(guān)關(guān)系,在編號(hào)為6的體檢數(shù)據(jù)丟失之前調(diào)查員甲已進(jìn)行相關(guān)的數(shù)據(jù)分析,并計(jì)算得出該組數(shù)據(jù)的線(xiàn)性回歸方程為![]() ,且根據(jù)回歸方程預(yù)估一名身高為180cm的員工體重為71kg,計(jì)算得到的其它數(shù)據(jù)如下:
,且根據(jù)回歸方程預(yù)估一名身高為180cm的員工體重為71kg,計(jì)算得到的其它數(shù)據(jù)如下:![]() ,
,![]() .
.
①求![]() 的值及表格中8名員工體重的平均值
的值及表格中8名員工體重的平均值![]() .
.
②在數(shù)據(jù)處理時(shí),調(diào)查員乙發(fā)現(xiàn)編號(hào)為8的員工體重?cái)?shù)據(jù)有誤,應(yīng)為63kg,身高數(shù)據(jù)無(wú)誤,請(qǐng)你根據(jù)調(diào)查員乙更正的數(shù)據(jù)重新計(jì)算線(xiàn)性回歸方程,并據(jù)此預(yù)估一名身高為180cm的員工的體重.
附:對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線(xiàn)
,其回歸直線(xiàn)![]() 的斜率和截距的最小二乘法估計(jì)分別為:
的斜率和截距的最小二乘法估計(jì)分別為: 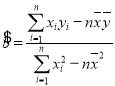 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
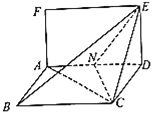
【題目】已知矩形![]() 和菱形
和菱形![]() 所在平面互相垂直,如圖,其中
所在平面互相垂直,如圖,其中![]() ,
, ![]() ,
, ![]() ,點(diǎn)
,點(diǎn)![]() 為線(xiàn)段
為線(xiàn)段![]() 的中點(diǎn).
的中點(diǎn).
(Ⅰ)試問(wèn)在線(xiàn)段![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得直線(xiàn)
,使得直線(xiàn)![]() 平面
平面![]() ?若存在,請(qǐng)證明
?若存在,請(qǐng)證明![]() 平面
平面![]() ,并求出
,并求出![]() 的值,若不存在,請(qǐng)說(shuō)明理由;
的值,若不存在,請(qǐng)說(shuō)明理由;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】下列命題中假命題是( )
A.若隨機(jī)變量![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,
,![]() ,則
,則![]() ;
;
B.已知直線(xiàn)![]() 平面
平面![]() ,直線(xiàn)
,直線(xiàn)![]() 平面
平面![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
C.若![]() ,則
,則![]() 在
在![]() 方向上的正射影的數(shù)量為
方向上的正射影的數(shù)量為![]()
D.命題![]() 的否定
的否定![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】“二進(jìn)制”來(lái)源于我國(guó)古代的《易經(jīng)》,該書(shū)中有兩類(lèi)最基本的符號(hào):“─”和“﹣﹣”,其中“─”在二進(jìn)制中記作“1”,“﹣﹣”在二進(jìn)制中記作“0”.如符號(hào)“”對(duì)應(yīng)的二進(jìn)制數(shù)011(2)化為十進(jìn)制的計(jì)算如下:011(2)=0×22+1×21+1×20=3(10).若從兩類(lèi)符號(hào)中任取2個(gè)符號(hào)進(jìn)行排列,則得到的二進(jìn)制數(shù)所對(duì)應(yīng)的十進(jìn)制數(shù)大于2的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() 的圖象在點(diǎn)
的圖象在點(diǎn)![]() 處的切線(xiàn)斜率為
處的切線(xiàn)斜率為![]() ,其中
,其中![]() 為自然對(duì)數(shù)的底數(shù).
為自然對(duì)數(shù)的底數(shù).
(1)求實(shí)數(shù)![]() 的值,并求
的值,并求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
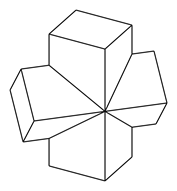
【題目】如圖是某機(jī)械零件的幾何結(jié)構(gòu),該幾何體是由兩個(gè)相同的直四棱柱組合而成的,且前后、左右、上下均對(duì)稱(chēng),每個(gè)四棱柱的底面都是邊長(zhǎng)為2的正方形,高為4,且兩個(gè)四棱柱的側(cè)棱互相垂直.則這個(gè)幾何體有________個(gè)面,其體積為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】盲盒里面通常裝的是動(dòng)漫、影視作品的周邊,或者設(shè)計(jì)師單獨(dú)設(shè)計(jì)出來(lái)的玩偶.由于盒子上沒(méi)有標(biāo)注,購(gòu)買(mǎi)者只有打開(kāi)才會(huì)知道自己買(mǎi)到了什么,因此這種驚喜吸引了眾多年輕人,形成了“盲盒經(jīng)濟(jì)”.某款盲盒內(nèi)可能裝有某一套玩偶的![]() 、
、![]() 、
、![]() 三種樣式,且每個(gè)盲盒只裝一個(gè).
三種樣式,且每個(gè)盲盒只裝一個(gè).
(1)若每個(gè)盲盒裝有![]() 、
、![]() 、
、![]() 三種樣式玩偶的概率相同.某同學(xué)已經(jīng)有了
三種樣式玩偶的概率相同.某同學(xué)已經(jīng)有了![]() 樣式的玩偶,若他再購(gòu)買(mǎi)兩個(gè)這款盲盒,恰好能收集齊這三種樣式的概率是多少?
樣式的玩偶,若他再購(gòu)買(mǎi)兩個(gè)這款盲盒,恰好能收集齊這三種樣式的概率是多少?
(2)某銷(xiāo)售網(wǎng)點(diǎn)為調(diào)查該款盲盒的受歡迎程度,隨機(jī)發(fā)放了200份問(wèn)卷,并全部收回.經(jīng)統(tǒng)計(jì),有![]() 的人購(gòu)買(mǎi)了該款盲盒,在這些購(gòu)買(mǎi)者當(dāng)中,女生占
的人購(gòu)買(mǎi)了該款盲盒,在這些購(gòu)買(mǎi)者當(dāng)中,女生占![]() ;而在未購(gòu)買(mǎi)者當(dāng)中,男生女生各占
;而在未購(gòu)買(mǎi)者當(dāng)中,男生女生各占![]() .請(qǐng)根據(jù)以上信息填寫(xiě)下表,并分析是否有
.請(qǐng)根據(jù)以上信息填寫(xiě)下表,并分析是否有![]() 的把握認(rèn)為購(gòu)買(mǎi)該款盲盒與性別有關(guān)?
的把握認(rèn)為購(gòu)買(mǎi)該款盲盒與性別有關(guān)?
女生 | 男生 | 總計(jì) | |
購(gòu)買(mǎi) | |||
未購(gòu)買(mǎi) | |||
總計(jì) |
參考公式: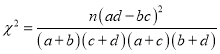 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)該銷(xiāo)售網(wǎng)點(diǎn)已經(jīng)售賣(mài)該款盲盒6周,并記錄了銷(xiāo)售情況,如下表:
周數(shù) | 1 | 2 | 3 | 4 | 5 | 6 |
盒數(shù) | 16 | ______ | 23 | 25 | 26 | 30 |
由于電腦故障,第二周數(shù)據(jù)現(xiàn)已丟失,該銷(xiāo)售網(wǎng)點(diǎn)負(fù)責(zé)人決定用第4、5、6周的數(shù)據(jù)求線(xiàn)性回歸方程,再用第1、3周數(shù)據(jù)進(jìn)行檢驗(yàn).
①請(qǐng)用4、5、6周的數(shù)據(jù)求出![]() 關(guān)于
關(guān)于![]() 的線(xiàn)性回歸方程
的線(xiàn)性回歸方程![]() ;
;
(注: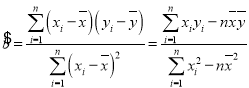 ,
,![]() )
)
②若由線(xiàn)性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過(guò)2盒,則認(rèn)為得到的線(xiàn)性回歸方程是可靠的,試問(wèn)①中所得的線(xiàn)性回歸方程是否可靠?
③如果通過(guò)②的檢驗(yàn)得到的回歸直線(xiàn)方程可靠,我們可以認(rèn)為第2周賣(mài)出的盒數(shù)誤差也不超過(guò)2盒,請(qǐng)你求出第2周賣(mài)出的盒數(shù)的可能取值;如果不可靠,請(qǐng)你設(shè)計(jì)一個(gè)估計(jì)第2周賣(mài)出的盒數(shù)的方案.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com