
【題目】已知實數(shù)![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值是2,則
上的最大值是2,則![]() ______
______
【答案】![]() 或
或![]()
【解析】
由題意可得f(0)≤2,求得a的范圍,去掉一個絕對值,再由最值的取得在頂點和端點處,計算得a的值,再檢驗可得a的值.
因為函數(shù)f(x)=|x2+|x﹣a|﹣3|在區(qū)間[﹣1,1]上的最大值是2,可得f(0)≤2,
且a>0,得|a﹣3|≤2,解得1≤a≤5,即有f(x)=|x2﹣x+a﹣3|,﹣1≤x≤1,
由f(x)的最大值在頂點或端點處取得,
當f(﹣1)=2,即|a﹣1|=2,解得a=3或﹣1(舍去);
當f(1)=2,即|a﹣3|=2,解得a=5或a=1;
當f(![]() )=2,即|a﹣
)=2,即|a﹣![]() |=2,解得a=
|=2,解得a=![]() 或
或![]() (舍去).
(舍去).
當a=1時,f(x)=|x2﹣x﹣2|,因為f(![]() )=
)=![]() >2,不符題意;(舍去).
>2,不符題意;(舍去).
當a=5時,f(x)=|x2﹣x+2|,因為f(-1)=4>2,不符題意;(舍去).
當a=3時,f(x)=|x2﹣x|,顯然當x=﹣1時,取得最大值2,符合題意;
當a=![]() 時,f(x)=|x2﹣x﹣
時,f(x)=|x2﹣x﹣![]() |,f(1)=
|,f(1)=![]() ,f(﹣1)=
,f(﹣1)=![]() ,f(
,f(![]() )=2,符合題意.
)=2,符合題意.
故答案為:3或![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】現(xiàn)有9位身高各異的同學(xué)拍照留念,分成前后兩排,前排4人,后排5人,要求每排同學(xué)的身高從中間到兩邊依次遞減,則不同的排隊方式有________種.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖在四棱錐![]() 中,平面
中,平面![]() 底面ABCD,底面ABCD是等腰梯形,
底面ABCD,底面ABCD是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]()
![]() .
.
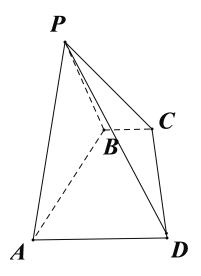
(1)證明:![]() .
.
(2)求平面PCD與平面PAB夾角(銳角)的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直角![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上一點,且滿足
上一點,且滿足![]() 平分
平分![]() ,
,![]() ,以
,以![]() 為折痕將
為折痕將![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.
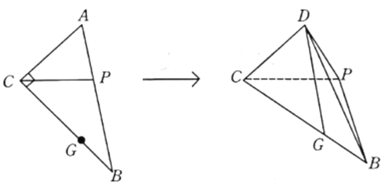
(1)證明:![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場一年中各月份的收入、支出(單位:萬元)情況的統(tǒng)計如折線圖所示,則下列說法正確的是( )
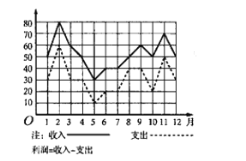
A.2至3月份的收入的變化率與11至12月份的收入的變化率相同
B.支出最高值與支出最低值的比是![]()
C.第三季度平均收入為60萬元
D.利潤最高的月份是2月份
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,焦距為2,直線
,焦距為2,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
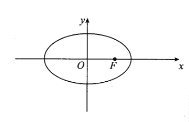
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 過橢圓的右焦點
過橢圓的右焦點![]() ,且
,且![]() ,求直線
,求直線![]() 方程;
方程;
(3)設(shè)![]() 為坐標原點,直線
為坐標原點,直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,若
,若![]() ,求
,求![]() 面積
面積![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() 若滿足:①對任意
若滿足:①對任意![]() 、
、![]() ,都有
,都有![]() ;②對任意
;②對任意![]() ,都有
,都有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“中心捺函數(shù)”,其中點
為“中心捺函數(shù)”,其中點![]() 稱為函數(shù)
稱為函數(shù)![]() 的中心.已知函數(shù)
的中心.已知函數(shù)![]() 是以
是以![]() 為中心的“中心捺函數(shù)”,若滿足不等式
為中心的“中心捺函數(shù)”,若滿足不等式![]() ,當
,當![]() 時,
時,![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知曲線C的極坐標方程是![]() ,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,曲線C經(jīng)過伸縮變換
,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,曲線C經(jīng)過伸縮變換 得到曲線E,直線
得到曲線E,直線 (t為參數(shù))與曲線E交于A,B兩點.
(t為參數(shù))與曲線E交于A,B兩點.
(1)設(shè)曲線C上任一點為![]() ,求
,求![]() 的最小值;
的最小值;
(2)求出曲線E的直角坐標方程,并求出直線l被曲線E截得的弦AB長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的右焦點的坐標為
的右焦點的坐標為![]() ,且長軸長為短軸長的
,且長軸長為短軸長的![]() 倍.橢圓
倍.橢圓![]() 的上、下頂點分別為
的上、下頂點分別為![]() ,經(jīng)過點
,經(jīng)過點![]() 的直線
的直線![]() 與橢圓相交于
與橢圓相交于![]() 兩點(不同于
兩點(不同于![]() 兩點).
兩點).
(1)求橢圓的方程;
(2)若直線![]() ,求點
,求點![]() 的坐標;
的坐標;
(3)設(shè)直線![]() 相交于點
相交于點![]() ,求證:
,求證:![]() 是定值.
是定值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com