
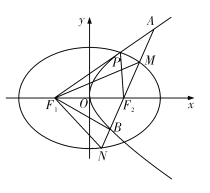
【題目】如圖,已知曲線![]() ,曲線
,曲線![]() 的左右焦點是
的左右焦點是![]() ,
, ![]() ,且
,且![]() 就是
就是![]() 的焦點,點
的焦點,點![]() 是
是![]() 與
與![]() 的在第一象限內的公共點且
的在第一象限內的公共點且![]() ,過
,過![]() 的直線
的直線![]() 分別與曲線
分別與曲線![]() 、
、![]() 交于點
交于點![]() 和
和![]() .
.
(Ⅰ)求點![]() 的坐標及
的坐標及![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 面積分別是
面積分別是![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ) ![]() .
.
【解析】試題分析:(Ⅰ)由![]() ,設
,設![]() ,據題意有
,據題意有![]() ,可求出點
,可求出點![]() 的坐標,將點
的坐標,將點![]() 的坐標代入橢圓方程,結合
的坐標代入橢圓方程,結合![]() ,列方程組,解出
,列方程組,解出![]() 的值即可得結果;(Ⅱ)易知
的值即可得結果;(Ⅱ)易知![]() ,當
,當![]() 不垂直于
不垂直于![]() 軸時,設
軸時,設![]() 的方程是
的方程是![]() ,聯立
,聯立![]() ,得
,得![]() ,根據韋達定理以及拋物線焦半徑公式可得
,根據韋達定理以及拋物線焦半徑公式可得![]() ,聯立
,聯立![]() 得:
得: ![]() ,根據韋達定理及弦長公式可得
,根據韋達定理及弦長公式可得![]() ,
, ![]() ,結合斜率不存在的情況可得結果.
,結合斜率不存在的情況可得結果.
試題解析:(Ⅰ) ![]() ,設
,設![]() ,據題意有
,據題意有![]() ,
,
則![]() ,
, 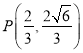 ,
,
點![]() 在橢圓上及
在橢圓上及![]() 就是
就是![]() 的焦點,則
的焦點,則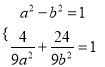 ,解之得:
,解之得: ![]() ,
,
所以![]() 的方程是
的方程是![]() .
.
或由![]() 計算出
計算出![]() ,從而得方程.
,從而得方程.
(Ⅱ)易知![]() ,當
,當![]() 不垂直于
不垂直于![]() 軸時,設
軸時,設![]() 的方程是
的方程是![]() ,
,
聯立![]() ,得
,得![]() ,
, ![]() ,
,
設![]() ,
, ![]() ,則
,則![]() ,
, ![]() ;
;
聯立![]() 得:
得: ![]() ,
,
![]()
![]() ,
,
設![]() ,
, ![]() ,
,
則![]() ,
, ![]() ,
,
![]() ,
,
(或![]() )
)
則![]() ,
,
當![]() 垂直于
垂直于![]() 軸時,易知
軸時,易知![]() ,
, ![]() ,此時
,此時![]() ,
,
綜上有![]() 的取值范圍是
的取值范圍是![]() .
.
設![]() 類似給分
類似給分


 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】在數列![]() 中,若
中,若![]() 是整數,且
是整數,且![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)若![]() ,
, ![]() ,寫出
,寫出![]() 的值;
的值;
(Ⅱ)若在數列![]() 的前2018項中,奇數的個數為
的前2018項中,奇數的個數為![]() ,求
,求![]() 得最大值;
得最大值;
(Ⅲ)若數列![]() 中,
中, ![]() 是奇數,
是奇數, ![]() ,證明:對任意
,證明:對任意![]() ,
, ![]() 不是4的倍數.
不是4的倍數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+ln(x-1),其中a為常數.
(1)試討論f(x)的單調區間;
(2)當a=![]() 時,存在x使得不等式
時,存在x使得不等式![]() 成立,求b的取值范圍.
成立,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖甲,在四邊形ABCD中, ![]() ,
, ![]() 是邊長為4的正三角形,把
是邊長為4的正三角形,把![]() 沿AC折起到
沿AC折起到![]() 的位置,使得平面PAC
的位置,使得平面PAC![]() 平面ACD,如圖乙所示,點
平面ACD,如圖乙所示,點![]() 分別為棱
分別為棱![]() 的中點.
的中點.
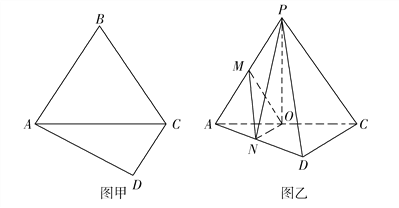
(1)求證: ![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題12分)如圖,在海岸線![]() 一側有一休閑游樂場,游樂場的前一部分邊界為曲線段
一側有一休閑游樂場,游樂場的前一部分邊界為曲線段![]() ,該曲線段是函數
,該曲線段是函數![]() ,
,![]() 的圖像,圖像的最高點為
的圖像,圖像的最高點為![]() .邊界的中間部分為長
.邊界的中間部分為長![]() 千米的直線段
千米的直線段![]() ,且
,且![]() .游樂場的后一部分邊界是以
.游樂場的后一部分邊界是以![]() 為圓心的一段圓弧
為圓心的一段圓弧![]() .
.

(1)求曲線段![]() 的函數表達式;
的函數表達式;
(2)曲線段![]() 上的入口
上的入口![]() 距海岸線
距海岸線![]() 最近距離為
最近距離為![]() 千米,現準備從入口
千米,現準備從入口![]() 修一條筆直的景觀路到
修一條筆直的景觀路到![]() ,求景觀路
,求景觀路![]() 長;
長;
(3)如圖,在扇形![]() 區域內建一個平行四邊形休閑區
區域內建一個平行四邊形休閑區![]() ,平行四邊形的一邊在海岸線
,平行四邊形的一邊在海岸線![]() 上,一邊在半徑
上,一邊在半徑![]() 上,另外一個頂點
上,另外一個頂點![]() 在圓弧
在圓弧![]() 上,且
上,且![]() ,求平行四邊形休閑區
,求平行四邊形休閑區![]() 面積的最大值及此時
面積的最大值及此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來鄭州空氣污染較為嚴重,現隨機抽取一年(365天)內100天的空氣中![]() 指數的監測數據,統計結果如下:
指數的監測數據,統計結果如下:
|
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
記某企業每天由空氣污染造成的經濟損失為![]() (單位:元),
(單位:元), ![]() 指數為
指數為![]() .當
.當![]() 在區間
在區間![]() 內時對企業沒有造成經濟損失;當
內時對企業沒有造成經濟損失;當![]() 在區間
在區間![]() 內時對企業造成經濟損失成直線模型(當
內時對企業造成經濟損失成直線模型(當![]() 指數為150時造成的經濟損失為500元,當
指數為150時造成的經濟損失為500元,當![]() 指數為200 時,造成的經濟損失為700元);當
指數為200 時,造成的經濟損失為700元);當![]() 指數大于300時造成的經濟損失為2000元.
指數大于300時造成的經濟損失為2000元.
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
(1)試寫出![]() 的表達式;
的表達式;
(2)試估計在本年內隨機抽取一天,該天經濟損失![]() 大于500元且不超過900元的概率;
大于500元且不超過900元的概率;
(3)若本次抽取的樣本數據有30天是在供暖季,其中有8天為重度污染,完成下面列聯表,并判斷是否有![]() 的把握認為鄭州市本年度空氣重度污染與供暖有關?
的把握認為鄭州市本年度空氣重度污染與供暖有關?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com