
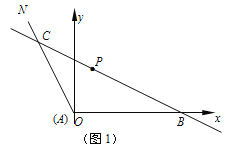
【題目】如圖,公路AM,AN圍成一塊頂角為α的角形耕地,其中tanα=-2,在該塊土地中P處有一小型建筑,經測量,它到公路AM,AN的距離分別為3km,![]() km,現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園,為盡量減少耕地占用,問如何確定B點的位置,使得該工業園區的面積最小?并求最小面積.
km,現要過點P修建一條直線公路BC,將三條公路圍成的區域ABC建成一個工業園,為盡量減少耕地占用,問如何確定B點的位置,使得該工業園區的面積最小?并求最小面積.

【答案】當AB=5km時,該工業園區的面積最小,最小面積為15km2.
【解析】
試題分析:先確定點P的位置,再利用BC的斜率表示工業園區的面積,利用導數求其最值.以A為原點,AB為x軸,建立平面直角坐標系.因為tanα=-2,故直線AN的方程是y=-2x.設點P(x0,y0).因為點P到AM的距離為3,故y0=3.由P到直線AN的距離為![]() ,得
,得![]() ,解得x0=1或x0=-4(舍去),所以點P(1,3).顯然直線BC的斜率存在.設直線BC的方程為y-3=k(x-1),k∈(-2,0).令y=0得xB=1-
,解得x0=1或x0=-4(舍去),所以點P(1,3).顯然直線BC的斜率存在.設直線BC的方程為y-3=k(x-1),k∈(-2,0).令y=0得xB=1-![]() .由
.由![]() 解得yC=
解得yC=![]() .設△ABC的面積為S,則S=
.設△ABC的面積為S,則S=![]() xB×yC=
xB×yC=![]() .由S=
.由S=![]() =0得k=-
=0得k=-![]() 或k=3.所以當k=-
或k=3.所以當k=-![]() 時,即AB=5時,S取極小值,也為最小值15.
時,即AB=5時,S取極小值,也為最小值15.
試題解析:解:如圖1,以A為原點,AB為x軸,建立平面直角坐標系.因為tanα=-2,故直線AN的方程是y=-2x.
設點P(x0,y0).
因為點P到AM的距離為3,故y0=3.
由P到直線AN的距離為![]() ,
,
得![]() ,解得x0=1或x0=-4(舍去),
,解得x0=1或x0=-4(舍去),
所以點P(1,3). 4分
顯然直線BC的斜率存在.設直線BC的方程為y-3=k(x-1),k∈(-2,0).
令y=0得xB=1-![]() . 6分
. 6分
由![]() 解得yC=
解得yC=![]() . 8分
. 8分
設△ABC的面積為S,則S=![]() ×xB×yC=
×xB×yC=![]() 10分
10分
由S=![]() =0得k=-
=0得k=-![]() 或k=3.
或k=3.
當-2<k<-![]() 時,S<0,S單調遞減;當-
時,S<0,S單調遞減;當-![]() <k<0時,S>0,S單調遞增. 13分
<k<0時,S>0,S單調遞增. 13分
所以當k=-![]() 時,即AB=5時,S取極小值,也為最小值15.
時,即AB=5時,S取極小值,也為最小值15.
答:當AB=5km時,該工業園區的面積最小,最小面積為15km2. 16分


科目:高中數學 來源: 題型:
【題目】已知定義在[0,1]上的函數f(x)滿足:
①f(0)=f(1)=0;
②對所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若對所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,則m的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,ABCD為矩形,平面PAD⊥平面ABCD. 
(1)求證:AB⊥PD;
(2)若∠BPC=90°,PB= ![]() ,PC=2,問AB為何值時,四棱錐P﹣ABCD的體積最大?并求此時平面BPC與平面DPC夾角的余弦值.
,PC=2,問AB為何值時,四棱錐P﹣ABCD的體積最大?并求此時平面BPC與平面DPC夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
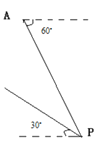
【題目】據監測,在海濱某城市附近的海面有一臺風. 臺風中心位于城市![]() 的東偏南
的東偏南![]() 方向、距離城市
方向、距離城市![]() 的海面
的海面![]() 處,并以
處,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移動(如圖示).如果臺風侵襲范圍為圓形區域,半徑
方向移動(如圖示).如果臺風侵襲范圍為圓形區域,半徑![]() ,臺風移動的方向與速度不變,那么該城市受臺風侵襲的時長為_____ .
,臺風移動的方向與速度不變,那么該城市受臺風侵襲的時長為_____ .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f0(x)= ![]() (x>0),設fn(x)為fn﹣1(x)的導數,n∈N* .
(x>0),設fn(x)為fn﹣1(x)的導數,n∈N* .
(1)求2f1( ![]() )+
)+ ![]() f2(
f2( ![]() )的值;
)的值;
(2)證明:對任意n∈N* , 等式|nfn﹣1( ![]() )+
)+ ![]() fn(
fn( ![]() )|=
)|= ![]() 都成立.
都成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面四邊形ABCD中,AD=1,CD=2,AC= ![]() .
. 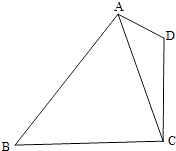
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高級中學共有學生2000名,各年級男、女生人數如下表:
高一年級 | 高二年級 | 高三年級 | |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
已知在全校學生中隨機抽取1名,抽到高二年級女生的概率是0.19.
(1)求![]() 的值;
的值;
(2)現用分層抽樣的方法在全校抽取48名學生,問應該在高三年級抽取多少名?
(3)已知![]() ,
,![]() ,求高三年級中女生比男生多的概率.
,求高三年級中女生比男生多的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從甲地到乙地要經過3個十字路口,設各路口信號燈工作相互獨立,且在各路口遇到紅燈的概率分別為![]() .
.
(Ⅰ)設![]() 表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量
表示一輛車從甲地到乙地遇到紅燈的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)若有2輛車獨立地從甲地到乙地,求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com