【題目】已知在正四棱錐P-ABCD中，側棱與底面成角為60°，且側面積為
，則四棱錐P-ABCD的內切球的表面積為（ ）
A.
B.
C.
D.
科目：高中數學 來源： 題型：
【題目】為迎接2022年冬奧會，北京市組織中學生開展冰雪運動的培訓活動，并在培訓結束后對學生進行了考核．記
表示學生的考核成績，并規定
為考核優秀．為了了解本次培訓活動的效果，在參加培訓的學生中隨機抽取了30名學生的考核成績，并作成如下莖葉圖：
（Ⅰ）從參加培訓的學生中隨機選取1人，請根據圖中數據，估計這名學生考核優秀的概率；
（Ⅱ）從圖中考核成績滿足
的學生中任取2人，求至少有一人考核優秀的概率；
（Ⅲ）記
表示學生的考核成績在區間
的概率，根據以往培訓數據，規定當
時培訓有效．請根據圖中數據，判斷此次中學生冰雪培訓活動是否有效，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】研究機構對某校學生往返校時間的統計資料表明：該校學生居住地到學校的距離
（單位：千米）和學生花費在上學路上的時間
（單位：分鐘）有如下的統計資料：
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明與有線性相關關系，試求：
（1）判斷與是否有很強的線性相關性？
（相關系數
的絕對值大于0.75時，認為兩個變量有很強的線性相關性，精確到0.01）
（2）求線性回歸方程
（精確到0.01）；
（3）將
分鐘的時間數據
稱為美麗數據，現從這6個時間數據中任取2個，求抽取的2個數據全部為美麗數據的概率.
參考數據：
，
，
，
，
，
參考公式：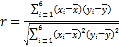
，
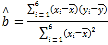
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】菜市房管局為了了解該市市民2018年1月至2019年1月期間購買二手房情況，首先隨機抽樣其中200名購房者，并對其購房面積
（單位：平方米，
）進行了一次調查統計，制成了如圖1所示的頻率分布南方匿，接著調查了該市2018年1月﹣2019年1月期間當月在售二手房均價
（單位：萬元/平方米），制成了如圖2所示的散點圖（圖中月份代碼1﹣13分別對應2018年1月至2019年1月）．
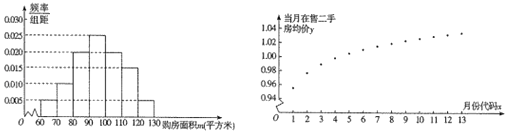
（1）試估計該市市民的平均購房面積
．
（2）現采用分層抽樣的方法從購房耐積位于
的40位市民中隨機取4人，再從這4人中隨機抽取2人，求這2人的購房面積恰好有一人在
的概率．
（3）根據散點圖選擇
和
兩個模型進行擬合，經過數據處理得到兩個回歸方程，分別為
和
，并得到一些統計量的值，如表所示：
|
| |
|
|
|
|
| |
請利用相關指數
判斷哪個模型的擬合效果更好，并用擬合效果更好的模型預測2019年6月份的二手房購房均價（精確到
參考數據：
，
，
，
，
,
,
,
．參考公式：相關指數
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4—4：坐標系與參數方程]
在平面直角坐標系
中，曲線
的參數方程為
（
為參數，
），以坐標原點
為極點，
軸的非負半軸為極軸，建立極坐標系，直線
的極坐標方程為
.
（1）設
是曲線上的一個動瞇，當
時，求點到直線的距離的最小值；
（2）若曲線上所有的點都在直線的右下方，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系xOy中，橢圓C：
(a＞b＞0)經過點(0，
)，點F是橢圓的右焦點，點F到左頂點的距離和到右準線的距離相等．過點F的直線
交橢圓于M，N兩點．
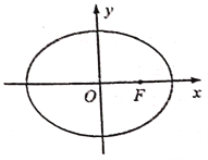
（1）求橢圓C的標準方程；
（2）當MF＝2FN時，求直線的方程；
（3）若直線上存在點P滿足PM·PN＝PF2，且點P在橢圓外，證明：點P在定直線上．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
