
【題目】已知![]() .
.
(1)求![]() 的單調區間;
的單調區間;
(2)當![]() 時,求證:對于
時,求證:對于![]() ,
,![]() 恒成立;
恒成立;
(3)若存在![]() ,使得當
,使得當![]() 時,恒有
時,恒有![]() 成立,試求
成立,試求![]() 的取值范圍.
的取值范圍.
【答案】(1)單調增區間為![]() ,單調減區間為
,單調減區間為![]() ;(2)詳見解析;(3)
;(2)詳見解析;(3)![]() .
.
【解析】
試題(1)對函數![]() 求導后,利用導數和單調性的關系,可求得函數
求導后,利用導數和單調性的關系,可求得函數![]() 的單調區間.(2)構造函數
的單調區間.(2)構造函數![]() ,利用導數求得函數
,利用導數求得函數![]() 在
在![]() 上遞減,且
上遞減,且![]() ,則
,則![]() ,故原不等式成立.(3)同(2)構造函數
,故原不等式成立.(3)同(2)構造函數![]() ,對
,對![]() 分成
分成![]() 三類,討論函數
三類,討論函數![]() 的單調性、極值和最值,由此求得
的單調性、極值和最值,由此求得![]() 的取值范圍.
的取值范圍.
試題解析:
(1)![]()
![]() ,
,
當![]() 時,
時,![]() .
.
解得![]() .
.
當![]() 時,解得
時,解得![]() .
.
所以![]() 單調增區間為
單調增區間為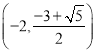 ,
,
單調減區間為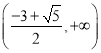 .
.
(2)設![]()
![]() ,
,
當![]() 時,由題意,當
時,由題意,當![]() 時,
時,
![]() 恒成立.
恒成立.
![]()
![]() ,
,
∴當![]() 時,
時,![]() 恒成立,
恒成立,![]() 單調遞減.
單調遞減.
又![]() ,
,
∴當![]() 時,
時,![]() 恒成立,即
恒成立,即![]() .
.
∴對于![]() ,
,![]() 恒成立.
恒成立.
(3)因為![]()
![]() .
.
由(2)知,當![]() 時,
時,![]() 恒成立,
恒成立,
即對于![]() ,
,![]() ,
,
不存在滿足條件的![]() ;
;
當![]() 時,對于
時,對于![]() ,
,![]() ,
,
此時![]() .
.
∴![]() ,
,
即![]() 恒成立,不存在滿足條件的
恒成立,不存在滿足條件的![]() ;
;
當![]() 時,令
時,令![]() ,
,
可知![]() 與
與![]() 符號相同,
符號相同,
當![]() 時,
時,![]() ,
,![]() ,
,
![]() 單調遞減.
單調遞減.
∴當![]() 時,
時,![]() ,
,
即![]() 恒成立.
恒成立.
綜上,![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 是橢圓
是橢圓![]() 上一點,
上一點,![]() 軸,
軸,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在合作學習小組的一次活動中,甲、乙、丙、丁、戊五位同學被隨機地分配承擔![]() ,
,![]() ,
,![]() ,
,![]() 四項不同的任務,每個同學只能承擔一項任務.
四項不同的任務,每個同學只能承擔一項任務.
(1)若每項任務至少安排一位同學承擔,求甲、乙兩人不同時承擔同一項任務的概率;
(2)設這五位同學中承擔任務![]() 的人數為隨機變量
的人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知若![]() ,則稱
,則稱![]() 為
為![]() 的原函數,此時
的原函數,此時![]() 所有的原函數為
所有的原函數為![]() ,其中
,其中![]() 為常數,如:
為常數,如:![]() ,則
,則![]() (
(![]() 為常數).現已知函數
為常數).現已知函數![]() 的導函數為
的導函數為![]() 且對任意的實數
且對任意的實數![]() 都有
都有![]() (
(![]() 是自然對數的底數),且
是自然對數的底數),且![]() ,若關于
,若關于![]() 的不等式
的不等式![]() 的解集中恰有兩個整數,則實數
的解集中恰有兩個整數,則實數![]() 的取值范圍是( )
的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市一次全市高中男生身高統計調查數據顯示:全市100000名男生的身高服從正態分布N(168,16).現從某學校高三年級男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于160 cm和184 cm之間,將測量結果按如下方式分成6組:第1組[160,164),第2組[164,168),…,第6組[180,184],如圖是按上述分組方法得到的頻率分布直方圖.
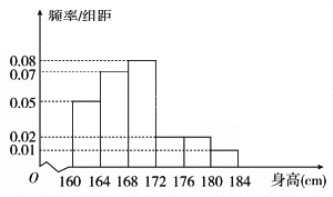
(1)由頻率分布直方圖估計該校高三年級男生平均身高狀況;
(2)求這50名男生身高在172 cm以上(含172 cm)的人數;
(3)在這50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,將該2人中身高排名(從高到低)在全市前130名的人數記為ξ,求ξ的數學期望.
參考數據:若ξ~N(μ,σ2),則P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com