
【題目】研究機構對某校學生往返校時間的統計資料表明:該校學生居住地到學校的距離![]() (單位:千米)和學生花費在上學路上的時間
(單位:千米)和學生花費在上學路上的時間![]() (單位:分鐘)有如下的統計資料:
(單位:分鐘)有如下的統計資料:
到學校的距離 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花費的時間 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果統計資料表明![]() 與
與![]() 有線性相關關系,試求:
有線性相關關系,試求:
(1)判斷![]() 與
與![]() 是否有很強的線性相關性?
是否有很強的線性相關性?
(相關系數![]() 的絕對值大于0.75時,認為兩個變量有很強的線性相關性,精確到0.01)
的絕對值大于0.75時,認為兩個變量有很強的線性相關性,精確到0.01)
(2)求線性回歸方程![]() (精確到0.01);
(精確到0.01);
(3)將![]() 分鐘的時間數據
分鐘的時間數據![]() 稱為美麗數據,現從這6個時間數據
稱為美麗數據,現從這6個時間數據![]() 中任取2個,求抽取的2個數據全部為美麗數據的概率.
中任取2個,求抽取的2個數據全部為美麗數據的概率.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
參考公式: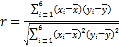 ,
,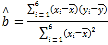
【答案】(1)![]() 與
與![]() 有很強的線性相關性;(2)
有很強的線性相關性;(2)![]() ;(3)
;(3)![]()
【解析】
(1)通過計算線性相關系數可得答案;(2)根據題意寫出統計表,用統計表中的數據求出橫標和縱標的平均數,利用最小二乘法做出線性回歸方程的系數![]() 、
、![]() ,寫出線性回歸方程;(3)根據(2)中求出的線性回歸方程,求出符合要求的數據個數,再列出全部情況,由古典概型的公式,求出所求概率.
,寫出線性回歸方程;(3)根據(2)中求出的線性回歸方程,求出符合要求的數據個數,再列出全部情況,由古典概型的公式,求出所求概率.
(1) ∴
∴![]() 與
與![]() 有很強的線性相關性
有很強的線性相關性
(2)依題意得![]()
![]() ,
,![]() ,
,![]()
所以
又因為![]()
故線性回歸方程為![]()
(3)由(2)可知,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,所以滿足
,所以滿足![]() 分鐘的美麗數據共有3個,設3個美麗數據為
分鐘的美麗數據共有3個,設3個美麗數據為![]() 、
、![]() 、
、![]() ,另3個不是美麗數據為
,另3個不是美麗數據為![]() 、
、![]() 、
、![]() ,則從6個數據中任取2個共有15種情況,即
,則從6個數據中任取2個共有15種情況,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,抽取到的數據全部為美麗數據的有3種情況,即
,其中,抽取到的數據全部為美麗數據的有3種情況,即![]() ,
,![]() ,
,![]() .所以從這6個數據
.所以從這6個數據![]() 中任取2個,抽取的2個數據全部為美麗數據的概率為
中任取2個,抽取的2個數據全部為美麗數據的概率為![]()


科目:高中數學 來源: 題型:
【題目】下列命題中:
①若命題![]() ,
,![]() ,則
,則![]() ,
,![]() ;
;
②將![]() 的圖象沿
的圖象沿![]() 軸向右平移
軸向右平移![]() 個單位,得到的圖象對應函數為
個單位,得到的圖象對應函數為![]() ;
;
③“![]() ”是“
”是“![]() ”的充分必要條件;
”的充分必要條件;
④已知![]() 為圓
為圓![]() 內異于圓心的一點,則直線
內異于圓心的一點,則直線![]() 與該圓相交.
與該圓相交.
其中正確的個數是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在第十五次全國國民閱讀調查中,某地區調查組獲得一個容量為![]() 的樣本,其中城鎮居民
的樣本,其中城鎮居民![]() 人,農村居民
人,農村居民![]() 人.在這些居民中,經常閱讀的城鎮居民
人.在這些居民中,經常閱讀的城鎮居民![]() 人,農村居民
人,農村居民![]() 人.
人.
(Ⅰ)填寫下面列聯表,并判斷是否有![]() 的把握認為,經常閱讀與居民居住地有關?
的把握認為,經常閱讀與居民居住地有關?
城鎮居民 | 農村居民 | 合計 | |
經常閱讀 |
|
| |
不經常閱讀 | |||
合計 |
|
(Ⅱ)從該地區居民城鎮的居民中,隨機抽取![]() 位居民參加一次閱讀交流活動,記這
位居民參加一次閱讀交流活動,記這![]() 位居民中經常閱讀的人數為
位居民中經常閱讀的人數為![]() ,若用樣本的頻率作為概率,求隨機變量
,若用樣本的頻率作為概率,求隨機變量![]() 的分布列和期望.
的分布列和期望.
附: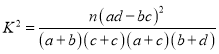 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面上給定相異兩點A,B,設P點在同一平面上且滿足![]() ,當
,當![]() 且
且![]() 時,P點的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,故我們稱這個圓為阿波羅尼斯圓,現有雙曲線
時,P點的軌跡是一個圓,這個軌跡最先由古希臘數學家阿波羅尼斯發現,故我們稱這個圓為阿波羅尼斯圓,現有雙曲線![]() (
(![]() ,
,![]() ),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足
),A,B為雙曲線的左、右頂點,C,D為雙曲線的虛軸端點,動點P滿足 ,
,![]() 面積的最大值為
面積的最大值為![]() ,
,![]() 面積的最小值為4,則雙曲線的離心率為______.
面積的最小值為4,則雙曲線的離心率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產某種產品,一條流水線年產量為![]() 件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
件,該生產線分為兩段,流水線第一段生產的半成品的質量指標會影響第二段生產成品的等級,具體見下表:
第一段生產的半成品質量指標 |
|
|
|
第二段生產的成品為一等品概率 | 0.2 | 0.4 | 0.6 |
第二段生產的成品為二等品概率 | 0.3 | 0.3 | 0.3 |
第二段生產的成品為三等品概率 | 0.5 | 0.3 | 0.1 |
從第一道生產工序抽樣調查了![]() 件,得到頻率分布直方圖如圖:
件,得到頻率分布直方圖如圖:

若生產一件一等品、二等品、三等品的利潤分別是![]() 元、
元、![]() 元、
元、![]() 元.
元.
(Ⅰ)以各組的中間值估計為該組半成品的質量指標,估算流水線第一段生產的半成品質量指標的平均值;
(Ⅱ)將頻率估計為概率,試估算一條流水線一年能為該公司創造的利潤;
(Ⅲ)現在市面上有一種設備可以安裝到流水線第一段,價格是![]() 萬元,使用壽命是
萬元,使用壽命是![]() 年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布
年,安裝這種設備后,流水線第一段半成品的質量指標服從正態分布![]() ,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
,且不影響產量.請你幫該公司作出決策,是否要購買該設備?說明理由.
(參考數據:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() 的方程為
的方程為![]() ,且圓
,且圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,設直線
兩點,設直線![]() 的方程為
的方程為![]() .
.
(1)當直線![]() 與圓
與圓![]() 相切時,求直線
相切時,求直線![]() 的方程;
的方程;
(2)已知直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點.(i)
兩點.(i)![]() ,求直線
,求直線![]() 的方程;(ii)直線
的方程;(ii)直線![]() 與直線
與直線![]() 相交于點
相交于點![]() ,直線
,直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,是否存在常數
,是否存在常數![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,點
為坐標原點,點![]() ,
,![]() ,過點
,過點![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .設點
.設點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求曲線![]() 的方程;
的方程;
(Ⅱ)已知直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,且與曲線
,且與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() 的中點為
的中點為![]() ,求三角形
,求三角形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,
,![]() 是橢圓
是橢圓![]() 上一點,
上一點,![]() 軸,
軸,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com