
【題目】在直角坐標系xOy中,直線l的參數方程為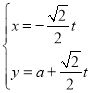 (t為參數,a∈R),以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ
(t為參數,a∈R),以O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ
(1)求直線l的普通方程及曲線C的直角坐標方程;
(2)若直線l過點P(1,1)且與曲線C交于AB兩點,求|PA|+|PB|
【答案】(1)l:x+y﹣a=0,C:y2=2x;(2)![]()
【解析】
(1) 消去參數t可得直線l的普通方程,利用極坐標與直角坐標的公式化簡求解可得曲線C的直角坐標方程
(2)設直線l的參數方程為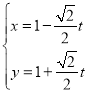 ,再代入拋物線的方程,利用直線參數方程的幾何意義求解即可.
,再代入拋物線的方程,利用直線參數方程的幾何意義求解即可.
(1)由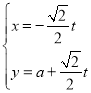 消去參數t可得直線l的普通方程為:x+y﹣a=0,
消去參數t可得直線l的普通方程為:x+y﹣a=0,
由ρsin2θ=2cosθ得ρ2sin2θ=2ρcosθ可得曲線C的直角坐標方程為:y2=2x.
(2)將P(1,1)代入x+y﹣a=0可得a=2,
所以直線l的參數方程為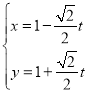 (t為參數)
(t為參數)
將其代入曲線C的普通方程得:t2+4![]() ﹣2=0,設A,B對應的參數為t1,t2,
﹣2=0,設A,B對應的參數為t1,t2,
則t1+t2=﹣4![]() ,t1t2=﹣2<0,∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|=
,t1t2=﹣2<0,∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|=![]() =
=![]() =
=![]() .
.


科目:高中數學 來源: 題型:
【題目】某房產銷售公司從登記購房的客戶中隨機選取了50名客戶進行調查,按他們購一套房的價格(萬元)分成6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到頻率分布直方圖如圖所示.用頻率估計概率.
得到頻率分布直方圖如圖所示.用頻率估計概率.
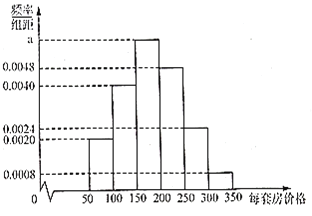
房產銷售公司每賣出一套房,房地產商給銷售公司的傭金如下表(單位:萬元):
房價區(qū)間 |
|
|
|
|
|
|
傭金收入 | 1 | 2 | 3 | 4 | 5 | 6 |
(1)求![]() 的值;
的值;
(2)求房產銷售公司賣出一套房的平均傭金;
(3)若該銷售公司平均每天銷售4套房,請估計公司月(按30天計)利潤(利潤=總傭金-銷售成本).
該房產銷售公司每月(按30天計)的銷售成本占總傭金的百分比按下表分段累計/span>計算:
月總傭金 | 不超過100萬元的部分 | 超過100萬元至200萬元的部分 | 超過200萬元至300萬元的部分 | 超過300萬元的部分 |
銷售成本占 傭金比例 |
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a≤8.函數f(x)=a1nx﹣x2+5,g(x)=2x+![]()
(1)若f(x)的極大值為5,求a的值
(2)若關于x的不等式f(x)≤g(x)在區(qū)間[1,+∞)上恒成立,求a的取值范圍,(1n2≈0.7)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|2x﹣3|+|x+2|
(1)求不等式f(x)≤5的解集;
(2)若關于x的不等式f(x)≤a﹣|x|在區(qū)間[﹣1,2]上恒成立,求實數a的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一件剛出土的珍貴文物要在博物館大廳中央展出,需要設計各面是玻璃平面的無底正四棱柱將其罩住,罩內充滿保護文物的無色氣體.已知文物近似于塔形,高1.8米,體積0.5立方米,其底部是直徑為0.9米的圓形,要求文物底部與玻璃罩底邊至少間隔0.3米,文物頂部與玻璃罩上底面至少間隔0.2米,氣體每立方米1000元,則氣體費用最少為( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com