【題目】已知
，
，
，
是半徑為2的球面上的點(diǎn)，
，
，點(diǎn)在
上的射影為
，則三棱錐
體積的最大值是（ ）.
A.
B.
C.
D.
【答案】B
【解析】
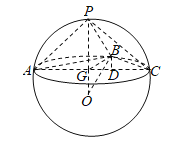
由
可以判斷出點(diǎn)
在底面的射影的位置，這樣可以確定球心位置，利用勾股定理、直角三角形的性質(zhì)可以求出點(diǎn)到底面
的距離，利用相似三角形的性質(zhì)，可以求出三角形的面積表達(dá)式，最后利用導(dǎo)數(shù)求出其面積的最大值，最后也就求出了體積的最大值,
因?yàn)?/span>，
，所以點(diǎn)在底面的射影
是直角三角形
斜邊
中點(diǎn)，所以球心
在線段
的延長(zhǎng)線上，設(shè)
，因此
，
，即
，
.
過(guò)
作
，垂足為
，設(shè)
，
，
，
由
，可得
，
，
設(shè)
，則有
，由
，可得
，
當(dāng)
時(shí)，
，函數(shù)單調(diào)遞增，
當(dāng)
時(shí)，
，函數(shù)單調(diào)遞減，故當(dāng)，函數(shù)有最大值，最大值為：
.三角形的面積的最大值為
.
三棱錐
體積的最大值是
.
故選：B
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某品牌汽車4S店，對(duì)該品牌旗下的A型、B型、C型汽車進(jìn)行維修保養(yǎng)，汽車4S店記錄了100輛該品牌三種類型汽車的維修情況，整理得下表：
車型 | A型 | B型 | C型 |
頻數(shù) | 20 | 40 | 40 |
假設(shè)該店采用分層抽樣的方法從上述維修的100輛該品牌三種類型汽車中隨機(jī)取10輛進(jìn)行問(wèn)卷回訪．
（1）求A型、B型、C型各車型汽車抽取的數(shù)目；
（2）維修結(jié)束后這100輛汽車的司機(jī)采用“100分制”打分的方式表示對(duì)4S店的滿意度，按照大于等于80為優(yōu)秀，小于80為合格，得到如下列聯(lián)表：
優(yōu)秀 | 合格 | 合計(jì) | |
男司機(jī) | 10 | 38 | 48 |
女司機(jī) | 25 | 27 | 52 |
合計(jì) | 35 | 65 | 100 |
問(wèn)能否在犯錯(cuò)誤概率不超過(guò)0.01的前提下認(rèn)為司機(jī)對(duì)4S店滿意度與性別有關(guān)系？請(qǐng)說(shuō)明原因．
（參考公式：
）
附表：
| 0.100 | 0.050 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】在直角坐標(biāo)系xOy中，直線l的參數(shù)方程為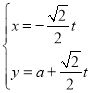
（t為參數(shù)，a∈R），以O為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，曲線C的極坐標(biāo)方程為ρsin2θ＝2cosθ
（1）求直線l的普通方程及曲線C的直角坐標(biāo)方程；
（2）若直線l過(guò)點(diǎn)P（1，1）且與曲線C交于AB兩點(diǎn)，求|PA|+|PB|
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】某汽車美容公司為吸引顧客，推出優(yōu)惠活動(dòng)：對(duì)首次消費(fèi)的顧客，按200元/次收費(fèi)，并注冊(cè)成為會(huì)員，對(duì)會(huì)員逐次消費(fèi)給予相應(yīng)優(yōu)惠，標(biāo)準(zhǔn)如下：
消費(fèi)次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
收費(fèi)比率 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
該公司注冊(cè)的會(huì)員中沒(méi)有消費(fèi)超過(guò)5次的，從注冊(cè)的會(huì)員中，隨機(jī)抽取了100位進(jìn)行統(tǒng)計(jì)，得到統(tǒng)計(jì)數(shù)據(jù)
如下：
消費(fèi)次數(shù) | 1次 | 2次 | 3次 | 4次 | 5次 |
人數(shù) | 60 | 20 | 10 | 5 | 5 |
假設(shè)汽車美容一次，公司成本為150元，根據(jù)所給數(shù)據(jù)，解答下列問(wèn)題：
（1）某會(huì)員僅消費(fèi)兩次，求這兩次消費(fèi)中，公司獲得的平均利潤(rùn)；
（2）以事件發(fā)生的頻率作為相應(yīng)事件發(fā)生的概率， 設(shè)該公司為一位會(huì)員服務(wù)的平均利潤(rùn)為
元，求大于40的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知
為常數(shù)， 
，函數(shù)
， 
（其中
是自然對(duì)數(shù)的底數(shù)）.
（1）過(guò)坐標(biāo)原點(diǎn)
作曲線
的切線，設(shè)切點(diǎn)為
，求證： 
；
（2）令
，若函數(shù)
在區(qū)間
上是單調(diào)函數(shù)，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知函數(shù)
在
處的切線方程為
.
（1）求函數(shù)
的解析式；
（2）若關(guān)于
的方程f（x）＝kex（其中e為自然對(duì)數(shù)的底數(shù)）恰有兩個(gè)不同的實(shí)根，求實(shí)數(shù)
的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】已知函數(shù)
且a≠0）．
（1）求曲線y=f（x）在點(diǎn)（1，f（1））處的切線方程；
（2）若函數(shù)f（x）的極小值為
，試求a的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來(lái)源： 題型：
【題目】
年
月，中國(guó)良渚古城遺址獲準(zhǔn)列入世界遺產(chǎn)名錄，標(biāo)志著中華五千年文明史得到國(guó)際社會(huì)認(rèn)可．良渚古城遺址是人類早期城市文明的范例，實(shí)證了中華五千年文明史．考古科學(xué)家在測(cè)定遺址年齡的過(guò)程中利用了“放射性物質(zhì)因衰變而減少”這一規(guī)律．已知樣本中碳
的質(zhì)量
隨時(shí)間
（單位：年）的衰變規(guī)律滿足
（
表示碳原有的質(zhì)量），則經(jīng)過(guò)
年后，碳的質(zhì)量變?yōu)樵瓉?lái)的________；經(jīng)過(guò)測(cè)定，良渚古城遺址文物樣本中碳的質(zhì)量是原來(lái)的
至
，據(jù)此推測(cè)良渚古城存在的時(shí)期距今約在________年到年之間．（參考數(shù)據(jù)：
）
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com
