
【題目】若a>0,b>0,且 ![]() .
.
(I) 求a3+b3的最小值;
(Ⅱ)是否存在a,b,使得2a+3b=6?并說明理由.
【答案】【解答】解:(Ⅰ)∵a>0,b>0,且 ![]() +
+ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() +
+ ![]() ≥2
≥2 ![]() ,∴ab≥2,
,∴ab≥2,
當且僅當a=b= ![]() 時取等號.
時取等號.
∵a3+b3 ≥2 ![]() ≥2
≥2 ![]() =4
=4 ![]() ,當且僅當a=b=
,當且僅當a=b= ![]() 時取等號,
時取等號,
∴a3+b3的最小值為4 ![]() .
.
(Ⅱ)∵2a+3b≥2 ![]() =2
=2 ![]() ,當且僅當2a=3b時,取等號.
,當且僅當2a=3b時,取等號.
而由(1)可知,2 ![]() ≥2
≥2 ![]() =4
=4 ![]() >6,
>6,
故不存在a,b,使得2a+3b=6成立.
【解析】(1)兩次連續代入![]() 公式,注意“=”成立條件是:當且僅當a=b.
公式,注意“=”成立條件是:當且僅當a=b.
(2)同樣代入![]() 公式,此時“=”成立的條件是2a=3b,與題目a=b不同,故不成立。
公式,此時“=”成立的條件是2a=3b,與題目a=b不同,故不成立。
【考點精析】利用基本不等式對題目進行判斷即可得到答案,需要熟知基本不等式:![]()
![]() ,(當且僅當
,(當且僅當![]() 時取到等號);變形公式:
時取到等號);變形公式:![]()
![]() .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】給出關于雙曲線的三個命題:
①雙曲線 ![]() ﹣
﹣ ![]() =1的漸近線方程是y=±
=1的漸近線方程是y=± ![]() x;
x;
②若點(2,3)在焦距為4的雙曲線 ![]() ﹣
﹣ ![]() =1上,則此雙曲線的離心率e=2;
=1上,則此雙曲線的離心率e=2;
③若點F,B分別是雙曲線 ![]() ﹣
﹣ ![]() =1的一個焦點和虛軸的一個端點,則線段FB的中點一定不在此雙曲線的漸近線上.
=1的一個焦點和虛軸的一個端點,則線段FB的中點一定不在此雙曲線的漸近線上.
其中正確命題的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,四邊形ABCD的各頂點均在橢圓E上,且對角線AC,BD均過坐標原點O,點D(2,1),AC,BD的斜率之積為
,四邊形ABCD的各頂點均在橢圓E上,且對角線AC,BD均過坐標原點O,點D(2,1),AC,BD的斜率之積為 ![]() .
.
(Ⅰ)求橢圓E的方程;
(Ⅱ)過D作直線l平行于AC.若直線l′平行于BD,且與橢圓E交于不同的兩點M.N,與直線l交于點P.
⑴證明:直線l與橢圓E有且只有一個公共點;
⑵證明:存在常數λ,使得|PD|2=λ|PM||PN|,并求出λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ ![]() ax2+bx+1的圖象在x=1處的切線l過點(
ax2+bx+1的圖象在x=1處的切線l過點( ![]() ,
, ![]() ).
).
(1)若函數g(x)=f(x)﹣(a﹣1)x(a>0),求g(x)最大值(用a表示);
(2)若a=﹣4,f(x1)+f(x2)+x1+x2+3x1x2=2,證明:x1+x2≥ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在數列{an}中,首項 ![]() ,前n項和為Sn , 且
,前n項和為Sn , 且 ![]()
(1)求數列{an}的通項
(2)如果bn=3(n+1)×2nan , 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產A,B兩種產品,生產每一噸產品所需的勞動力、煤和電如下表:
產品品種 | 勞動力(個) | 煤(噸) | 電(千瓦時) |
A產品 | 3 | 9 | 4 |
B產品 | 10 | 4 | 5 |
已知生產每噸A產品的利潤是7萬元,生產每噸B產品的利潤是12萬元,現因條件限制,該企業僅有勞動力300個,煤360噸,并且供電局只能供電200千瓦時,試問該企業如何安排生產,才能獲得最大利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若圖,在三棱柱 ![]() 中,平面
中,平面 ![]() 平面
平面 ![]() ,且
,且 ![]() 和
和 ![]() 均為正三角形.
均為正三角形.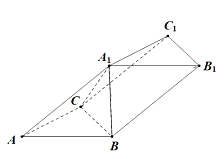
(1)在 ![]() 上找一點
上找一點 ![]() ,使得
,使得 ![]() 平面
平面 ![]() ,并說明理由.
,并說明理由.
(2)若 ![]() 的面積為
的面積為 ![]() ,求四棱錐
,求四棱錐 ![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形 ![]() 中,
中, ![]() ,
, ![]() ,點
,點 ![]() 是
是 ![]() 上的動點.現將矩形
上的動點.現將矩形 ![]() 沿著對角線
沿著對角線 ![]() 折成二面角
折成二面角 ![]() ,使得
,使得 ![]() .
.
(Ⅰ)求證:當 ![]() 時,
時, ![]() ;
;
(Ⅱ)試求 ![]() 的長,使得二面角
的長,使得二面角 ![]() 的大小為
的大小為 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com