
【題目】如果![]() 的定義域為
的定義域為![]() ,對于定義域內的任意
,對于定義域內的任意![]() ,存在實數
,存在實數![]() 使得
使得![]() 成立,則稱此函數具有“
成立,則稱此函數具有“![]() 性質”.給出下列命題:
性質”.給出下列命題:
①函數![]() 具有“
具有“![]() 性質”;
性質”;
②若奇函數![]() 具有“
具有“![]() 性質”,且
性質”,且![]() ,則
,則![]() ;
;
③若函數![]() 具有“
具有“![]() 性質”,圖象關于點
性質”,圖象關于點![]() 成中心對稱,且在
成中心對稱,且在![]() 上單調遞減,則
上單調遞減,則![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
④若不恒為零的函數![]() 同時具有“
同時具有“![]() 性質”和“
性質”和“![]() 性質”,且函數
性質”,且函數![]() 對
對![]() ,都有
,都有![]()
![]() 成立,則函數
成立,則函數![]() 是周期函數.
是周期函數.
其中正確的是__________(寫出所有正確命題的編號).
 星級口算天天練系列答案
星級口算天天練系列答案科目:高中數學 來源: 題型:
【題目】自2016年1月1日起,我國全面二孩政策正式實施,這次人口與生育政策的歷史性調整,使得“要不要再生一個”,“生二孩能休多久產假”等問題成為千千萬萬個家庭在生育決策上避不開的話題.為了解針對產假的不同安排方案形成的生育意愿,某調查機構隨機抽取了200戶有生育二胎能力的適齡家庭進行問卷調查,得到如下數據:
產假安排(單位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭數 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中數據所得的頻率代替概率,面對產假為14周與16周,估計某家庭有生育意愿的概率分別為多少?
(2)假設從5種不同安排方案中,隨機抽取2種不同安排分別作為備選方案,然后由單位根據單位情況自主選擇.
①求兩種安排方案休假周數和不低于32周的概率;
②如果用![]() 表示兩種方案休假周數之和.求隨機變量
表示兩種方案休假周數之和.求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() 是函數
是函數![]() 的導函數,則
的導函數,則![]() 的圖象大致是( )
的圖象大致是( )
A. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/8f50d3dfba9b485fac00e42a95909498.png] B. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/74ae44978a70424c961e850ed79072da.png]
C. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/2f113f7ec5294ba0bbd1f66b13f3e152.png] D. [Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395356672/STEM/dbaa9025ccdb497380b769e5396c4c19.png]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據統計,某5家鮮花店今年4月的銷售額和利潤額資料如下表:
鮮花店名稱 | A | B | C | D | E |
銷售額x(千元) | 3 | 5 | 6 | 7 | 9 |
利潤額y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法計算利潤額y關于銷售額x的回歸直線方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鮮花店的銷售額為8千元時,利用(1)的結論估計這家鮮花店的利潤額是多少.
參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計值公式分別為
中斜率和截距的最小二乘法估計值公式分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求![]() 的值域;
的值域;
(3)求![]() 的遞增區間
的遞增區間
(4)求![]() 的對稱軸;
的對稱軸;
(5)求![]() 的對稱中心;
的對稱中心;
(6)![]() 的三邊a,b,c滿足
的三邊a,b,c滿足![]() ,且b所對的角為x,求x的取值范圍及函數
,且b所對的角為x,求x的取值范圍及函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著“一帶一路”倡議的推進,中國與沿線國家旅游合作越來越密切,中國到“一帶一路”沿線國家的游客人也越來越多,如圖是2013-2018年中國到“一帶一路”沿線國家的游客人次情況,則下列說法正確的是( )
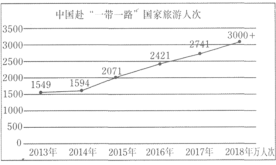
①2013-2018年中國到“一帶一路”沿線國家的游客人次逐年增加
②2013-2018年這6年中,2016年中國到“一帶一路”沿線國家的游客人次增幅最小
③2016-2018年這3年中,中國到“一帶一路”沿線國家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com